
分析 由α≤α-5cosβ,得到cosβ<0,由已知α≤t,即$t≥\frac{2co{s}^{3}β}{2-cosβ}$,令$f(t)=\frac{2co{s}^{3}β}{2-cosβ}$,则f′(t)=$\frac{4co{s}^{2}βsinβ(2cosβ-3)}{(2-cosβ)^{2}}$,令f′(t)=0,则sinβ=0,当sinβ=0时,f(t)取得最小值,然后由t≤α-5cosβ,即$t≤\frac{2co{s}^{3}β+5co{s}^{2}β}{2-cosβ}$,令$f(t)=\frac{2co{s}^{3}β+5co{s}^{2}β}{2-cosβ}$,则${f}^{′}(t)=\frac{cosβsinβ(-7cosβ+4co{s}^{2}β-20)}{(2-cosβ)^{2}}$.令f′(t)=0,则sinβ=0.当sinβ=0时,f(t)取得最大值.
解答 解:∵α≤α-5cosβ,
∴0≤-5cosβ.∴cosβ<0.
∵α≤t,∴$t≥co{s}^{3}β+\frac{t}{2}cosβ$,即$t≥\frac{2co{s}^{3}β}{2-cosβ}$.
令$f(t)=\frac{2co{s}^{3}β}{2-cosβ}$,则f′(t)=$\frac{-6co{s}^{2}βsinβ(2-cosβ)-2co{s}^{3}βsinβ}{(2-cosβ)^{2}}$=$\frac{4co{s}^{2}βsinβ(2cosβ-3)}{(2-cosβ)^{2}}$,
令f′(t)=0,则sinβ=0.
∴当sinβ=0时,f(t)取得最小值.f(t)=$\frac{-2}{2+1}=-\frac{2}{3}$.
∵t≤α-5cosβ,∴α≥t+5cosβ.
∴$t≤co{s}^{3}β+\frac{t+5cosβ}{2}cosβ$即$t≤\frac{2co{s}^{3}β+5co{s}^{2}β}{2-cosβ}$.
令$f(t)=\frac{2co{s}^{3}β+5co{s}^{2}β}{2-cosβ}$,则${f}^{′}(t)=\frac{cosβsinβ(-7cosβ+4co{s}^{2}β-20)}{(2-cosβ)^{2}}$.
令f′(t)=0,则sinβ=0.
当sinβ=0时,f(t)取得最大值.f(t)=$\frac{-2+5}{2+1}=1$.
则实数t的取值范围是:[$-\frac{2}{3}$,1].
故答案为:[$-\frac{2}{3}$,1].
点评 本题考查了三角函数的恒等变换应用,考查了导数的综合运用,计算量大,具有一定的难度,是难题.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
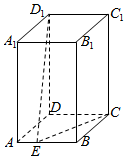 如图,在四棱柱ABCD-A1B1C1D1中,底面是ABCD正方形,侧棱AA1⊥底面ABCD.已知AB=1,E为AB上一个动点,当D1E+CE取得最小值$\sqrt{10}$时,三棱锥D1-ADE的外接球表面积为$\frac{40π}{9}$.
如图,在四棱柱ABCD-A1B1C1D1中,底面是ABCD正方形,侧棱AA1⊥底面ABCD.已知AB=1,E为AB上一个动点,当D1E+CE取得最小值$\sqrt{10}$时,三棱锥D1-ADE的外接球表面积为$\frac{40π}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
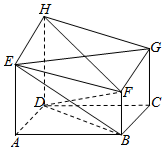 如图,六面体ABCDHEFG中,四边形ABCD为菱形,AE,BF,CG,DH都垂直于平面ABCD,若DA=DH=DB=4,AE=CG=3
如图,六面体ABCDHEFG中,四边形ABCD为菱形,AE,BF,CG,DH都垂直于平面ABCD,若DA=DH=DB=4,AE=CG=3查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{2}$+1 | C. | $\sqrt{2}$+2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com