
分析 由题意可设正三角形的边长为a,侧棱为h,根据体积关系可以求得h=$\frac{12}{{a}^{2}}$,即可求出正三角形的外接圆的半径为$\frac{\sqrt{3}}{3}$a,进而空间几何关系可以求得球O的半径关于a的关系式,通过整理,拆分,灵活运用基本不等式,即可求出最值,但应当注意运用基本不等式取得等号的条件.
解答 解:设正三角形的边长为a,侧棱为h,则$\frac{\sqrt{3}}{4}{a}^{2}h$=3$\sqrt{3}$,
∴h=$\frac{12}{{a}^{2}}$,
∵正三角形的外接圆的半径为$\frac{\sqrt{3}}{3}$a,
∴球O的半径r为$\sqrt{\frac{1}{3}{a}^{2}+\frac{36}{{a}^{4}}}$≥$\sqrt{3}$
当且仅当$\frac{1}{2}{a}^{2}=\frac{108}{{a}^{4}}$时,球O的半径取得最小值,即a=$\sqrt{6}$,(舍去负值).
∴球O的表面积的最小值为4πr2=12π.
故答案为:12π.
点评 本题考查空间几何体中位置关系、球和正棱柱的性质,考查学生的运算能力和空间形象能力,考查学生灵活运用基本不等式进行求解最值的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{3}{2}$)∪($\frac{3}{2}$,+∞) | B. | (-∞,0)∪($\frac{3}{2}$,+∞) | C. | (-∞,0)∪(1,+∞) | D. | ($\frac{3}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3+2\sqrt{2}}{2}$ | C. | 3$\sqrt{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
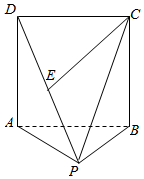 如图,P为正方体ABCD外一点,PB⊥平面ABCD,PB=AB=2,E为PD中点
如图,P为正方体ABCD外一点,PB⊥平面ABCD,PB=AB=2,E为PD中点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=8x | B. | x2=8y | C. | y2=4x | D. | x2=4y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 随着试验次数的增加,频率一般会越来越接近概率 | |
| B. | 频率是客观存在的,与试验次数无关 | |
| C. | 概率是随机的,在试验前不能确定 | |
| D. | 频率就是概率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com