
分析 (1)cosA=2$co{s}^{2}\frac{A}{2}$-1,sinA=$\sqrt{1-co{s}^{2}A}$.再利用数量积运算性质可得bc.利用面积计算公式即可得出.
(2)tanA=$\frac{4}{3}$,利用tan(A+B)=$\frac{tanA+tanB}{1-tanAtanB}$=-2.△ABC中,tanC=-tan(A+B),及其余弦定理即可得出.
解答 解:(1)cosA=2$co{s}^{2}\frac{A}{2}$-1=$\frac{3}{5}$,sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{4}{5}$.
∴bc×$\frac{3}{5}$=15,可得bc=25.
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}×25×\frac{4}{5}$=10.
(2)由tanA=$\frac{4}{3}$,tanB=2,∴tan(A+B)=$\frac{tanA+tanB}{1-tanAtanB}$=-2.
∴△ABC中,tanC=-tan(A+B)=2,
即B=C.∴b=c=5.
∴a2=b2+c2-2bccosA=20,解得a=2$\sqrt{5}$.
点评 本题考查了余弦定理、和差公式、数量积运算性质、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:高中数学 来源: 题型:选择题
| A. | y=f(x)的最小正周期是π,其图象关于$x=-\frac{π}{4}$对称 | |
| B. | y=f(x)的最小正周期是2π,其图象关于$x=\frac{π}{2}$对称 | |
| C. | y=f(x)的最小正周期是π,其图象关于$x=\frac{π}{2}$对称 | |
| D. | y=f(x)的最小正周期是2π,其图象关于$x=-\frac{π}{4}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,10) | B. | (10,2) | C. | (3,5) | D. | (5,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
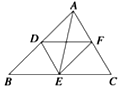
| A. | $\overrightarrow{AE}=\overrightarrow{AD}+\overrightarrow{FA}$ | B. | $\overrightarrow{DE}+\overrightarrow{AF}=0$ | C. | $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}≠0$ | D. | $\overrightarrow{DE}-\overrightarrow{DF}=\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com