
在空间直角坐标系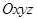 中,已知
中,已知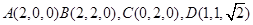 .若
.若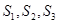 分别是三棱锥
分别是三棱锥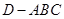 在
在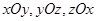 坐标平面上的正投影图形的面积,则( )
坐标平面上的正投影图形的面积,则( )
A.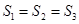 | B.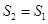 且 且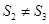 |
C.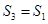 且 且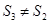 | D.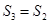 且 且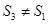 |
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知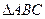 中∠ACB=90°,AS=BC=1,AC=2,SA⊥面ABC,AD⊥SC于D,
中∠ACB=90°,AS=BC=1,AC=2,SA⊥面ABC,AD⊥SC于D,
(1)求证: AD⊥面SBC;
(2)求二面角A-SB-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
若{a,b,c}为空间的一组基底,则下列各项中,能构成基底的一组向量是( )
| A.a,a+b,a-b | B.b,a+b,a-b |
| C.c,a+b,a-b | D.a+b,a-b,a+2b |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图,正方体ABCD-A1B1C1D1中,E,F分别在A1D,AC上,且A1E= A1D,AF=
A1D,AF=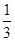 AC,则( )
AC,则( )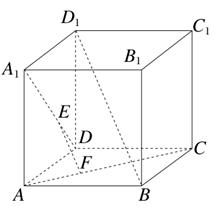
| A.EF至多与A1D,AC之一垂直 |
| B.EF⊥A1D,EF⊥AC |
| C.EF与BD1相交 |
| D.EF与BD1异面 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
在空间直角坐标系中,定义:平面α的一般方程为:Ax+By+Cz+D=0(A,B,C,D∈R,且A,B,C不同时为零),点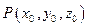 到平面α的距离为:
到平面α的距离为: ,则在底面边长与高都为2的正四棱锥中,底面中心O到侧面的距离等于( )
,则在底面边长与高都为2的正四棱锥中,底面中心O到侧面的距离等于( )
A. | B. | C. | D.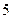 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
在正三棱柱ABC—A1B1C1中,D是AC的中点,AB1⊥BC1,则平面DBC1与平面CBC1所成的角为( )
| A.30° | B.45° | C.60° | D.90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com