
(本题满分12分)已知数列 的首项
的首项 ,
,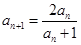 ,
,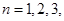 ….
….
(Ⅰ)证明:数列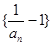 是等比数列;
是等比数列;
(Ⅱ)求数列 的前
的前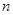 项和
项和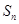 .
.
科目:高中数学 来源: 题型:解答题
(本题满分16分)
已知有穷数列 共有
共有 项(整数
项(整数 ),首项
),首项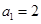 ,设该数列的前
,设该数列的前 项和为
项和为 ,且
,且 其中常数
其中常数 ⑴求
⑴求 的通项公式;⑵若
的通项公式;⑵若 ,数列
,数列 满足
满足
求证: ;
;
⑶若⑵中数列 满足不等式:
满足不等式: ,求
,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分) 已知曲线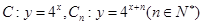 ,从
,从 上的点
上的点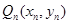 作
作 轴的垂线,交
轴的垂线,交 于点
于点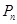 ,再从点
,再从点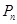 作
作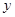 轴的垂线,交
轴的垂线,交 于点
于点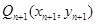 ,
,
设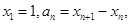
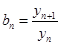 .。
.。 求数列
求数列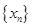 的通项公式;
的通项公式;  记
记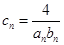 ,数列
,数列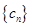 的前
的前 项和为
项和为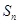 ,试比较
,试比较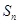 与
与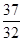 的大小
的大小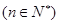 ;
;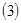 记
记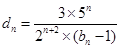 ,数列
,数列 的前
的前 项和为
项和为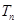 ,试证明:
,试证明: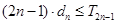 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知数列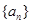 和
和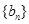 满足:
满足: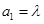 ,
,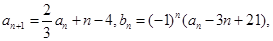 其中
其中 为实数,
为实数,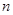 为正整数.
为正整数.
(1)对任意实数 ,证明数列
,证明数列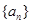 不是等比数列;
不是等比数列;
(2)试判断数列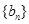 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
(3)设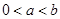 ,
,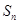 为数列
为数列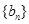 的前
的前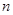 项和.是否存在实数
项和.是否存在实数 ,使得对任意正整数
,使得对任意正整数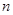 ,都有
,都有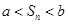 ?若存在,求
?若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某工厂用7万元钱购买了一台新机器,运输安装费用2千元,每年投保、动力消耗的费用也为2千元,每年的保养、维修、更换易损零件的费用逐年增加,第一年为2千元,第二年为3千元,第三年为4千元,依此类推,即每年增加1千元.问这台机器最佳使用年限是多少年?并求出年平均费用的最小值.(最佳使用年限佳是使年平均费用最小的时间)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com