
| A. | 相离 | B. | 相切 | ||
| C. | 相交 | D. | 随F值的变化而变化 |
分析 化圆的一般方程为标准方程,求出圆心坐标及半径,由圆心到直线的距离结合特殊值得答案.
解答 解:由x2+y2+2x+2y+F=0,得(x+1)2+(y+1)2=2-F(F<2),
圆心坐标为(-1,-1),半径为$\sqrt{2-F}$.
圆心到直线的距离d=$\frac{|-2-2+F|}{\sqrt{8}}=\frac{|4-F|}{2\sqrt{2}}=\frac{4-F}{2\sqrt{2}}$.
当F=0时,$\sqrt{2-F}=\frac{4-F}{2\sqrt{2}}$,直线与圆相切;
当F=1时,$\sqrt{2-F}=1<\frac{4-F}{2\sqrt{2}}$,直线与圆相离.
∴圆x2+y2+2x+2y+F=0与直线2x+2y+F=0的位置关系是随F值的变化而变化.
故选:D.
点评 本题考查直线与圆位置关系的应用,考查点到直线距离公式的应用,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
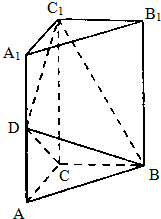 如图,三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=BC=$\frac{1}{2}$AA1,D是棱AA1的中点,DC1⊥BD.
如图,三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=BC=$\frac{1}{2}$AA1,D是棱AA1的中点,DC1⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2或-8 | B. | -2或8 | C. | 1或-9 | D. | -1或9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com