
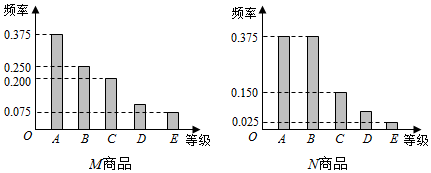
���� ��������������ʾ���N��Ʒ�ijɼ��ȼ�ΪD��Ƶ�ʺͲ�������M��N������Ʒ�������ɴ�����������ʾ���N��Ʒ�ijɼ��ȼ�ΪD�ļ����͵����ʾ���M��Ʒ�ɼ���ƽ���֣�
������������ʾ���M��Ʒ�ijɼ��ȼ�ΪD�ļ������Ӷ��õ�X�Ŀ���ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�EX��
��� �⣺�������ʾ���N��Ʒ�ijɼ��ȼ�ΪD��Ƶ��Ϊ��
1-0.025-0.150-0.375-0.375=0.075��
������ʾ���N��Ʒ�ijɼ��ȼ�ΪD�ļ���Ϊx��
��M��Ʒ�ijɼ��ȼ�ΪB����10������������M��N������Ʒ������ͬ��
���������M��N������Ʒ�������ǣ�$\frac{10}{0.250}$=40��
��$\frac{x}{40}=0.075$�����x=3��
�ߵȼ�A��B��C��D��E�ֱ��Ӧ5�֣�4�֣�3�֣�2�֣�1�֣�
������ʾ���M��Ʒ�ɼ���ƽ���֣�5��0.375+4��0.250+3��0.200+2����1-0.375-0.250-0.200-0.075��+1��0.075=3.75��
�������ʾ���M��Ʒ�ijɼ��ȼ�ΪD�ļ���Ϊ0.1��40=4��
��X�Ŀ���ȡֵΪ0��1��2��
P��X=0��=$\frac{{C}_{3}^{2}}{{C}_{7}^{2}}$=$\frac{3}{21}$=$\frac{1}{7}$��
P��X=1��=$\frac{{C}_{3}^{1}{C}_{4}^{1}}{{C}_{7}^{2}}$=$\frac{12}{21}$=$\frac{4}{7}$��
P��X=2��=$\frac{{C}_{4}^{2}}{{C}_{7}^{2}}$=$\frac{6}{21}$=$\frac{2}{7}$��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 |
| P | $\frac{1}{7}$ | $\frac{4}{7}$ | $\frac{2}{7}$ |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ɢ����������ķֲ��е������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
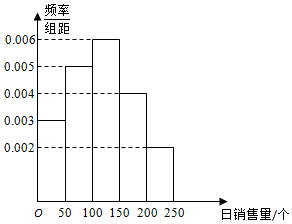 ��ͼ��ʾ��һ��������۵��������ij����������ۼ�¼������������������Ƶ�ʷֲ�ֱ��ͼ����һ������30����㣬������������һ��������������������150��������Ϊ9��
��ͼ��ʾ��һ��������۵��������ij����������ۼ�¼������������������Ƶ�ʷֲ�ֱ��ͼ����һ������30����㣬������������һ��������������������150��������Ϊ9���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���Vp����q | B�� | p�ģ��Vq�� | C�� | ���Vp���ģ��Vq�� | D�� | ���Vp����q |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2k | B�� | 2k+1 | C�� | 2k+2 | D�� | 2k-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
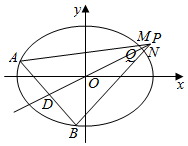 ��ͼ����ֱ֪��OP����ԲC��$\frac{{x}^{2}}{4{m}^{2}}$+$\frac{{y}^{2}}{3{m}^{2}}$=1�ڵ�Q������OΪ����ԭ�㣬��P������Ϊ��2��1����$\overrightarrow{OQ}$=$\frac{\sqrt{3}}{2}$$\overrightarrow{OP}$������ԲC������ԭ�����AB��ֱ��OPƽ���ڵ�D����ֱ��AP��BP����ԲC����һ����ֱ�ΪM��N��
��ͼ����ֱ֪��OP����ԲC��$\frac{{x}^{2}}{4{m}^{2}}$+$\frac{{y}^{2}}{3{m}^{2}}$=1�ڵ�Q������OΪ����ԭ�㣬��P������Ϊ��2��1����$\overrightarrow{OQ}$=$\frac{\sqrt{3}}{2}$$\overrightarrow{OP}$������ԲC������ԭ�����AB��ֱ��OPƽ���ڵ�D����ֱ��AP��BP����ԲC����һ����ֱ�ΪM��N���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com