练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

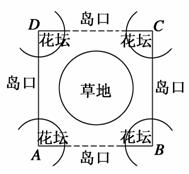
    如图，现要在边长为100 m的正方形ABCD内建一个交通“环岛”．以正方形的四个顶点为圆心在四个角分别建半径为x m(x不小于9)的扇形花坛，以正方形的中心为圆心建一个半径为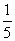x2 m的圆形草地．为了保证道路畅通，岛口宽不小于60 m，绕岛行驶的路宽均不小于10  m.

    (1)求x的取值范围；(运算中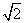取1.4)

    (2)若中间草地的造价为a元/m2，四个花坛的造价为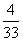ax元/m2，其余区域的造价为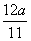元/m2，当x取何值时，可使“环岛”的整体造价最低？


    解　(1)由题意，得

    解得即9≤x≤15.

    (2)记“环岛”的整体造价为y元，则由题意，得

    令f(x)＝－x4＋x3－12x2，

    则f′(x)＝－x3＋4x2－24x

    ＝

    由f′(x)＝0，解得x＝10或x＝15.

    列表如下：

    ∴当x＝10，f(x)取极小值，即y取最小值．

    故当x＝10 m时，可使“环岛”的整体造价最低．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若a＝20.5，b＝logπ3，c＝log2sin，则(　　)

    A．b>c>a                                B．b>a>c

    C．a>b>c                                D．c>a>b

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝x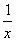＋(x∈(－∞，0)∪(0，＋∞))的图象为C1，C1关于点A(2,1)的对称的图象为C2，C2对应的函数为g(x)．

    (1)求函数y＝g(x)的解析式，并确定其定义域；

    (2)若直线y＝b与C2只有一个交点，求b的值，并求出交点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


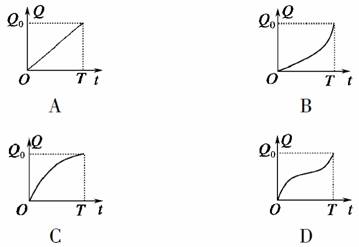
    物价上涨是当前的主要话题，特别是菜价，我国某部门为尽快实现稳定菜价，提出四种绿色运输方案．据预测，这四种方案均能在规定的时间T内完成预测的运输任务Q0，各种方案的运输总量Q与时间t的函数关系如图所示，在这四种方案中，运输效率(单位时间的运输量)逐步提高的是(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


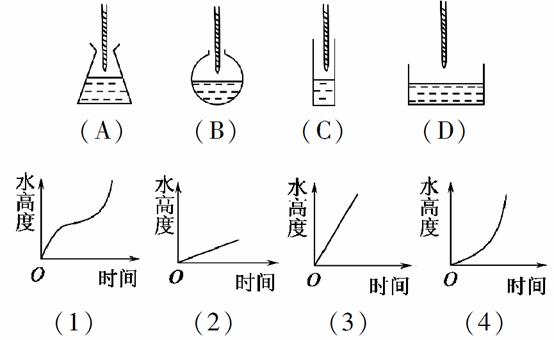
    生活经验告诉我们，当水注进容器(设单位时间内进水量相同)时，水的高度随着时间的变化而变化，在下图中请选择与容器相匹配的图象，(A)对应________；(B)对应________；(C)对应________；(D)对应________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)在R上满足f(x)＝2f(2－x)－x2＋8x－8，则曲线y＝f(x)在点(1，f(1))处切线的斜率是(　　)

    A．2                                    B．1

    C．3                                    D．－2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝xsinx＋cosx的图象在点(t，f(t))处切线的斜率为k，则函数k＝g(t)的部分图象为(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝－x2＋4x－3lnx在[t，t＋1]上不单调，则t的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    曲线y＝＋2x＋2e2x，直线x＝1，x＝e和x轴所围成的区域的面积是________．

    查看答案和解析>>

    同步练习册答案