
����AOB���Ľ�Ϊ60�㣬����Բ�뾶Ϊ ���������£��������ַ�ʽ���ڽӾ���CDEF��
���������£��������ַ�ʽ���ڽӾ���CDEF��
������CDEF�Ķ���C��D�����εİ뾶OB�ϣ�����E��Բ��AB�ϣ�����F�ڰ뾶OA�ϣ����EOB=�ȣ�
����M��Բ��AB���е㣬����CDEF�Ķ���D��E��Բ��AB�ϣ��ҹ���ֱ��OM�Գƣ�����C��F�ֱ��ڰ뾶OB��OA�ϣ����EOM=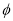 ��
��
���о����������ַ�ʽ�¾�����������ֵ����˵�����ַ�ʽ����һ�־���������
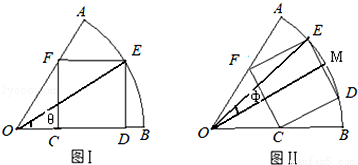
���ֵ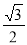
��������
���������(1)���ù�ʽʱҪע����鹫ʽ������������Ҫע��Ͳ���ǵ�����ԣ�Ҫע�����ݡ����ݵ�������ã���2���������Ǻ��������䣺����ָ��ǡ���������ʽ����ǣ��Խǵķֲ�Ҫ�����ܻ���ͬ����ͬ�ǡ�����ǣ������������ܼ��ٺ������ƣ���ʽ����ʽ�ӱ���һ��Ҫ����������������ʽ�������ʹ����ȣ��ʵ�ѡ��ʽ���б��Σ���3��������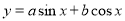 ��Ϊ
��Ϊ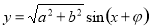 ���ɽ�һ���о����������ڡ������ԡ���ֵ�ͶԳ���.
���ɽ�һ���о����������ڡ������ԡ���ֵ�ͶԳ���.
��������� �⣨1���� �У���
����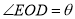 ����
����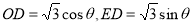
��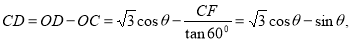


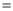

��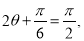 ��
�� ʱ��
ʱ��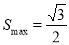
������ ��
�� �Ľ���Ϊ
�Ľ���Ϊ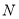 ��
��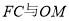 �Ľ���Ϊ
�Ľ���Ϊ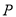 ����
���� ��
��
����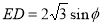 ����
����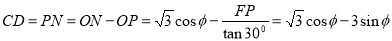
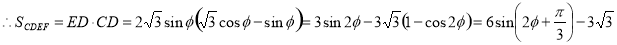
��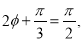 ��
��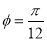 ʱ��
ʱ��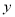 ȡ�����ֵ
ȡ�����ֵ .
.
 ,���������ַ�ʽ�¾�����������ֵΪ��ʽ
,���������ַ�ʽ�¾�����������ֵΪ��ʽ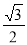

���㣺��ʵ������ת��Ϊ���Ǻ�������ֵ����.


 Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016��ɽ��ʡ�����и�һ3�����������ѧ�Ծ��������棩 ���ͣ�ѡ����
����һ��ֱ�ع鷽��Ϊ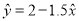 ,�����
,�����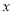 ����һ����λʱ ( )
����һ����λʱ ( )
A.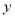 ƽ������1.5����λ B.
ƽ������1.5����λ B.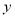 ƽ������2����λ
ƽ������2����λ
C.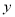 ƽ������1.5����λ D.
ƽ������1.5����λ D.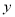 ƽ������2����λ
ƽ������2����λ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016��ɽ��ʡ��һ��ѧ����ĩģ�������ѧ�Ծ��������棩 ���ͣ�ѡ����
�� ����
���� ����
����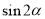 ��ֵΪ�� ��
��ֵΪ�� ��
A.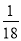 B.
B. C.
C.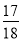 D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016��ɽ��ʡ��һ��ѧ����ĩģ����һ��ѧ�Ծ��������棩 ���ͣ������
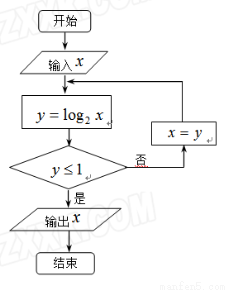
ִ����ͼ��ʾ�ij����ͼ�������� �������
�������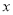 ��ֵΪ .
��ֵΪ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016��ɽ��ʡ��һ��ѧ����ĩģ����һ��ѧ�Ծ��������棩 ���ͣ�ѡ����
ijУ�����ݽ������У���λ��ίΪһѡ�ִ���ķ������£�
90 86 90 97 93 94 93
ȥ��һ����߷ֺ�һ����ͷֺ���ʣ���ݵ�ƽ��ֵ�ͷ���ֱ�Ϊ�� ��
A.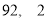 B.
B.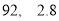 C.
C.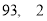 D.
D.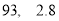
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016��ɽ��ʡ�����и�һ��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
������˵����
��1������y=��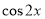 ����С�������ǦУ�
����С�������ǦУ�
��2���ձ��� ���ϵĽǵļ�����
���ϵĽǵļ�����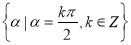 ��
��
��3������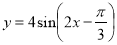 ��һ���Գ�����Ϊ
��һ���Գ�����Ϊ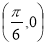
��4�����ABC��������������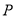 ��
��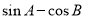 ��cos��A+B�����ڵ�����������ȷ���������� _________ ��
��cos��A+B�����ڵ�����������ȷ���������� _________ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016��ɽ��ʡ�����и�һ��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ��ij������ִ�������λ��ίΪ�ס�������ѡ�ִ�ֵľ�Ҷͼ������m������0��9�е�һ������ȥ��һ����߷ֺ�һ����ͷ�֮�ס�������ѡ�ֵķ���ֱ���a1��a2���� ��.

A��a1��a2 B��a1��a2
C��a1=a2 D��a1��a2�Ĵ�С��m��ֵ�й�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016��ɽ��ʡ��һ��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��֪ ����ʹsin
����ʹsin  =
= ������
������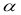 =
=
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016��ɽ��ʡ��ɽ�и�һ��ѧ���п�����ѧ�Ծ��������棩 ���ͣ������
��֪ ��
��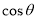 ����
���� ����������
����������
��1�� ����2��
����2�� ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com