
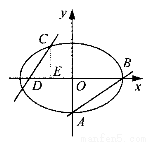
如图,已知椭圆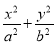 (a>b>0)的离心率
(a>b>0)的离心率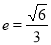 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为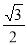 .
.
(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
(1)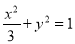 ;(2)
;(2)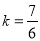 .
.
【解析】
试题分析:(1)设椭圆的方程,用待定系数法求出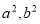 的值;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式
的值;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式 :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
试题解析:【解析】
(1)直线AB方程为:bx-ay-ab=0.
依题意 解得
解得 
∴椭圆方程为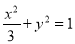 .[
.[
(2)假若存在这样的k值,由 得
得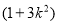
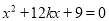 .
.
∴ 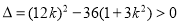 ①
①
设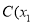 ,
,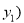 、
、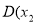 ,
,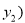 ,则
,则 ②
②
而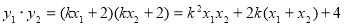 .
.
要使以CD为直径的圆过点E(-1,0),当且仅当CE⊥DE时,则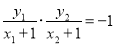 ,即
,即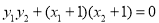 ∴
∴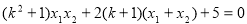 ③
③
将②式代入③整理解得 .经验证,
.经验证, ,使①成立.
,使①成立.
综上可知,存在 ,使得以CD为直径的圆过点E.
,使得以CD为直径的圆过点E.
考点:(1)椭圆的标准方程;(2)直线与椭圆的综合问题.


科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
某班有60名学生,一次考试后数学成绩ξ~N(110,102),若P(100≤ξ≤110)=0.35,则估计该班学生数学成绩在120分以上的人数为( ).
A.10 B.9 C.8 D.7
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试文科数学试卷(解析版) 题型:选择题
曲线y=e2x在点(0,1)处的切线方程为( ).
A.y= x+1 B.y=﹣2x+1 C.y=2x﹣1 D.y=2x+1
x+1 B.y=﹣2x+1 C.y=2x﹣1 D.y=2x+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com