
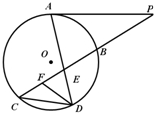
 如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=
如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=| DE |
| EC |
| FE |
| ED |
| DE2 |
| FE |
| 32 |
| 2 |
| 9 |
| 2 |
3×
| ||
| 3 |
| 9 |
| 2 |
| AE |
| EF |
| PE |
| ED |
| AE•ED |
| EF |
| ||
| 2 |
| 27 |
| 4 |
| 27 |
| 4 |
| 15 |
| 4 |
| 15 |
| 4 |
| 15 |
| 4 |
| 9 |
| 2 |
| 15×45 |
| 4×4 |
15
| ||
| 4 |
15
| ||
| 4 |


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
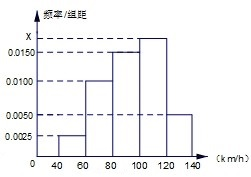 根据某固定测速点测得的某时段内过往的100辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h~120km/h,则该时段内过往的这100辆机动车中属非正常行驶的有
根据某固定测速点测得的某时段内过往的100辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h~120km/h,则该时段内过往的这100辆机动车中属非正常行驶的有查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
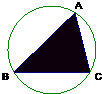 如图已知圆的半径为10,其内接三角形ABC的内角A、B分别为60°和45°,现向圆内随机撒一粒豆子,则豆子落在三角形ABC内的概率为( )
如图已知圆的半径为10,其内接三角形ABC的内角A、B分别为60°和45°,现向圆内随机撒一粒豆子,则豆子落在三角形ABC内的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| A、{x|x>0} |
| B、{x|x<-1或x>0} |
| C、{x|x>4} |
| D、{x|-1≤x≤4} |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、f(0)<f(6) |
| B、f(-3)>f(2) |
| C、f(-1)>f(3) |
| D、f(-2)<f(-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 喜欢 | 不喜欢 | 合计 | |
| 大于40岁 | 20 | 5 | 25 |
| 20岁至40岁 | 10 | 20 | 30 |
| 合计 | 30 | 25 | 55 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com