
计算
(1)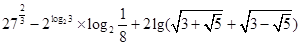 (2)
(2)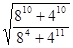
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:解答题
养路处建造无底的圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12米,高4米。养路处拟另建一个更大的圆锥形仓库,以存放更多食盐。现有两种方案:一是新建的仓库的底面直径比原来增加4米(高不变);二是高度增加4米(底面直径不变)。
分别计算按这两种方案所建的仓库的体积;
分别计算按这两种方案所建的仓库的表面积;
哪个方案更经济些?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
将52名志愿者分成A,B两组参加义务植树活动,A组种植150捆白杨树苗,B组种植200捆沙棘树苗.假定A,B两组同时开始种植.
(1)根据历年统计,每名志愿者种植一捆白杨树苗用时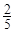 小时,种植一捆沙棘树苗用时
小时,种植一捆沙棘树苗用时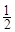 小时.应如何分配A,B两组的人数,使植树活动持续时间最短?
小时.应如何分配A,B两组的人数,使植树活动持续时间最短?
(2)在按(1)分配的人数种植1小时后发现,每名志愿者种植一捆白杨树苗用时仍为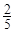 小时,而每名志愿者种植一捆沙棘树苗实际用时
小时,而每名志愿者种植一捆沙棘树苗实际用时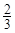 小时,于是从A组抽调6名志愿者加入B组继续种植,求植树活动所持续的时间.
小时,于是从A组抽调6名志愿者加入B组继续种植,求植树活动所持续的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
经市场调查:生产某产品需投入年固定成本为3万元,每生产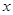 万件,需另投入流动成本为
万件,需另投入流动成本为 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,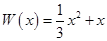 (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,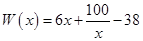 (万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(1)写出年利润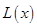 (万元)关于年产量
(万元)关于年产量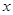 (万件)的函数解析式;
(万件)的函数解析式;
(注:年利润=年销售收入 固定成本
固定成本 流动成本)
流动成本)
(2)年产量为多少万件时,在这一商品的生产中所获利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,一水渠的横断面是抛物线形,O是抛物线的顶点,口宽EF=4米,高3米建立适当的直角坐标系,求抛物线方程.
现将水渠横断面改造成等腰梯形ABCD,要求高度不变,只挖土,不填土,求梯形ABCD的下底AB多大时,所挖的土最少? 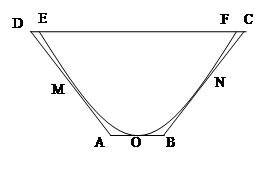
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位决定对本单位职工实行年医疗费用报销制度,拟制定年医疗总费用在2万元至10万元(包括2万元和10万元)的报销方案,该方案要求同时具备下列三个条件:①报销的医疗费用y(万元)随医疗总费用x(万元)增加而增加;②报销的医疗费用不得低于医疗总费用的50%;③报销的医疗费用不得超过8万元.
(1)请你分析该单位能否采用函数模型y=0.05(x2+4x+8)作为报销方案;
(2)若该单位决定采用函数模型y=x-2lnx+a(a为常数)作为报销方案,请你确定整数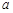 的值.(参考数据:ln2»0.69,ln10»2.3)
的值.(参考数据:ln2»0.69,ln10»2.3)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在某服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为20元,并且每周(7天)涨价2元,从第6周开始保持30元的价格平稳销售;从第12周开始,当季节即将过去时,平均每周减价2元,直到第16周周末,该服装不再销售。
⑴试建立销售价y与周次x之间的函数关系式;
⑵若这种时装每件进价Z与周次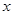 次之间的关系为Z=
次之间的关系为Z=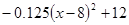 ,1≤
,1≤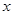 ≤16,且
≤16,且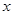 为整数,试问该服装第几周出售时,每件销售利润最大?最大利润为多少?
为整数,试问该服装第几周出售时,每件销售利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场销售某种商品的经验表明,该商品每日的销售量y (单位:千克)与销售价格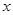 (单位:元/千克)满足关系式y=
(单位:元/千克)满足关系式y=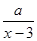 +10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
+10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求a的值;
(2)若该商品的成品为3元/千克, 试确定销售价格x的值, 使商场每日销售该商品所获得的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知甲、乙两个工厂在今年的1月份的利润都是6万,且乙厂在2月份的利润是8万元.若甲、乙两个工厂的利润(万元)与月份x之间的函数关系式分别符合下列函数模型:f(x)=a1x2—4x+6,g(x)=a2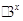 +b2(a1,a2,b2∈R).
+b2(a1,a2,b2∈R).
(1)求函数f(x)与g(x)的解析式;
(2)求甲、乙两个工厂今年5月份的利润;
(3)在同一直角坐标系下画出函数f(x)与g(x)的草图,并根据草图比较今年1—10月份甲、乙两个工厂的利润的大小情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com