
O为坐标原点,F为抛物线C:y2=4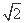 x的焦点,P为C上一点,若|PF|=4
x的焦点,P为C上一点,若|PF|=4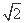 ,则△POF的面积为( )
,则△POF的面积为( )
(A)2 (B)2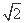 (C)2
(C)2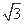 (D)4
(D)4
科目:高中数学 来源: 题型:
给定函数①y=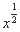 ,②y=
,②y=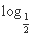 (x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是( )
(x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是( )
(A)①② (B)②③
(C)③④ (D)①④
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)=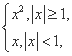 g(x)是二次函数.若f[g(x)]的值域是[0,+∞),则g(x)的值域是( )
g(x)是二次函数.若f[g(x)]的值域是[0,+∞),则g(x)的值域是( )
(A)(-∞,-1]∪[1,+∞) (B)(-∞,-1]∪[0,+∞)(C)[0,+∞) (D)[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=x2-4x+3,g(x)=3x-2,集合M={x∈R|f(g(x))>0},N={x∈R|g(x)<2},则M∩N为( )
(A)(1,+∞) (B)(0,1)
(C)(-1,1) (D)(-∞,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
幂函数y=x-1及直线y=x,y=1,x=1将平面直角坐标系的第一象限分成八个“卦限”:①,②,③,④,⑤,⑥,⑦,⑧(如图所示),那么幂函数y=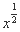 的图象经过的“卦限”是( )
的图象经过的“卦限”是( )
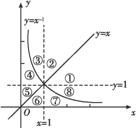
(A)④⑦ (B)④⑧ (C)③⑧ (D)①⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点A(4,4)在抛物线y2=px(p>0)上,该抛物线的焦点为F,过点A作直线l:x=- 的垂线,垂足为M,则∠MAF的平分线所在直线的方程为 .
的垂线,垂足为M,则∠MAF的平分线所在直线的方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,AB为☉O直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.证明:

(1)∠FEB=∠CEB;
(2)EF2=AD·BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com