
【题目】在平面直角坐标系xOy中,曲线![]() :
:![]() =0(a>0),曲线
=0(a>0),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系;
为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系;
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)已知极坐标方程为![]() =
=![]() 的直线与曲线
的直线与曲线![]() ,
,![]() 分别相交于P,Q两点(均异于原点O),若|PQ|=
分别相交于P,Q两点(均异于原点O),若|PQ|=![]() ﹣1,求实数a的值;
﹣1,求实数a的值;
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日“世界读书日”来临之际,某校为了了解中学生课外阅读情况,随机抽取了
日“世界读书日”来临之际,某校为了了解中学生课外阅读情况,随机抽取了![]() 名学生,并获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表.
名学生,并获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表.
组号 | 分组 | 频数 | 频率 |
1 | [0,5) | 5 | 0.05 |
2 | [5,10) | a | 0.35 |
3 | [10,15) | 30 | b |
4 | [15,20) | 20 | 0.20 |
5 | [20,25] | 10 | 0.10 |
合计 | 100 | 1 | |
(1)求![]() 、
、![]() 的值
的值
(2)作出这些数据的频率分布直方图

(3)假设每组数据组间是平均分布的,试估计该组数据的平均数和中位数.(同一组中的数据用该组区间的中点值作代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行四边形![]() 所在平面与直角梯形
所在平面与直角梯形![]() 所在平面互相垂直,且
所在平面互相垂直,且![]() ,
,![]() 为
为![]() 中点.
中点.
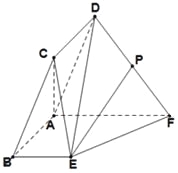
(1)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(2)求平面![]() 与平面
与平面![]() 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() +1(
+1(![]() )在(0,+∞)内有且只有一个零点,则
)在(0,+∞)内有且只有一个零点,则![]() 在[﹣1,1]上的值域为
在[﹣1,1]上的值域为
A. [﹣4,0] B. [﹣4,1] C. [﹣1,3] D. [﹣![]() ,12]
,12]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 中有:①若
中有:①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() —定为等腰三角形;③若
—定为等腰三角形;③若![]() ,则
,则![]() —定为直角三角形;④若
—定为直角三角形;④若![]() ,且该三角形有两解,则
,且该三角形有两解,则![]() 的范围是
的范围是![]() .以上结论中正确的个数有( )
.以上结论中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() ,圆
,圆![]() 是以
是以![]() 的中点为圆心,
的中点为圆心,![]() 为半径的圆.
为半径的圆.
(1)若圆![]() 的切线在
的切线在![]() 轴和
轴和![]() 轴上截距相等,求切线方程;
轴上截距相等,求切线方程;
(2)若![]() 是圆
是圆![]() 外一点,从
外一点,从![]() 向圆
向圆![]() 引切线
引切线![]() ,
,![]() 为切点,
为切点,![]() 为坐标原点,
为坐标原点,![]() ,求使
,求使![]() 最小的点
最小的点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com