
【题目】如图,已知四边形![]() 是正方形,
是正方形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 都是等边三角形,
都是等边三角形, ![]() 、
、![]() 、
、![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 、
、![]() 、
、![]() 的中点,分别以
的中点,分别以![]() 、
、![]() 、
、![]() 、
、![]() 为折痕将四个等边三角形折起,使得
为折痕将四个等边三角形折起,使得![]() 、
、![]() 、
、![]() 、
、![]() 四点重合于一点
四点重合于一点![]() ,得到一个四棱锥.对于下面四个结论:
,得到一个四棱锥.对于下面四个结论:
①![]() 与
与![]() 为异面直线; ②直线
为异面直线; ②直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]()
③![]() 平面
平面![]() ; ④平面
; ④平面![]() 平面
平面![]() ;
;
其中正确结论的个数有( )

A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
【答案】D
【解析】①错误.所得四棱锥中,设![]() 中点为
中点为![]() ,则
,则![]() 、
、![]() 两点重合,∵
两点重合,∵![]() ,即
,即![]() ,即
,即![]() 与
与![]() 不是异面直线;②正确.∵
不是异面直线;②正确.∵![]() ,
, ![]() 与
与![]() 重合,且
重合,且![]() 与
与![]() 所成角为
所成角为![]() ,说明
,说明![]() 与
与![]() 所成角为
所成角为![]() ;③正确.∵
;③正确.∵![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ;④正确.∵
;④正确.∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() 点,∴平面
点,∴平面![]() 平面
平面![]() ,即平面
,即平面![]() 平面
平面![]() ,故选
,故选![]() .
.
【 方法点睛】本题主要通过对多个命题真假的判断,主要综合考查线线成角、线面成角、线面平行以及面面平行的判断,属于难题.这种题型综合性较强,也是高考的命题热点,同学们往往因为某一处知识点掌握不好而导致“全盘皆输”,因此做这类题目更要细心、多读题,尽量挖掘出题目中的隐含条件,另外,要注意从简单的自己已经掌握的知识点入手,然后集中精力突破较难的命题.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的方程为:
的方程为: ![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
(![]() )当
)当![]() 时,求直线
时,求直线![]() 被圆
被圆![]() 截得的弦长;
截得的弦长;
(![]() )当直线
)当直线![]() 被圆
被圆![]() 截得的弦长最短时,求直线
截得的弦长最短时,求直线![]() 的方程;
的方程;
(![]() )在(
)在(![]() )的前提下,若
)的前提下,若![]() 为直线
为直线![]() 上的动点,且圆
上的动点,且圆![]() 上存在两个不同的点到点
上存在两个不同的点到点![]() 的距离为
的距离为![]() ,求点
,求点![]() 的横坐标的取值范围.
的横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图.则产品数量位于[55,65)范围内的频率为;这20名工人中一天生产该产品数量在[55,75)的人数是 . 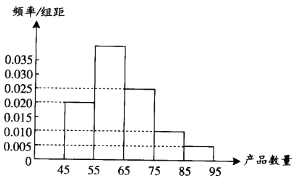
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半圆![]() 的直径为
的直径为![]() ,
, ![]() 为直径延长线上的一点,
为直径延长线上的一点, ![]() ,
, ![]() 为半圆上任意一点,以
为半圆上任意一点,以![]() 为一边作等边三角形
为一边作等边三角形![]() ,设
,设![]()
![]() .
.
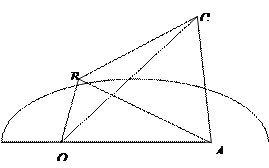
(1)当![]() 为何值时,四边形
为何值时,四边形![]() 面积最大,最大值为多少;
面积最大,最大值为多少;
(2)当![]() 为何值时,
为何值时, ![]() 长最大,最大值为多少.
长最大,最大值为多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为正整数,数列
为正整数,数列![]() 满足
满足![]() ,
, ![]() ,设数列
,设数列![]() 满足
满足![]()
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)若数列![]() 是等差数列,求实数
是等差数列,求实数![]() 的值;
的值;
(3)若数列![]() 是等差数列,前
是等差数列,前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,求满足条件的所有整数
成立,求满足条件的所有整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)过点(
=1(a>b>0)过点( ![]() ,1),且以椭圆短轴的两个端点和一个焦点为顶点的三角形是等腰直角三角形.
,1),且以椭圆短轴的两个端点和一个焦点为顶点的三角形是等腰直角三角形.
(1)求椭圆的标准方程;
(2)设M(x,y)是椭圆C上的动点,P(p,0)是x轴上的定点,求|MP|的最小值及取最小值时点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018海南高三阶段性测试(二模)】如图,在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上一动点.
上一动点.
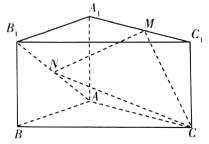
(I)是否存在一点![]() ,使得线段
,使得线段![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
(II)若点![]() 为
为![]() 的中点且
的中点且![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
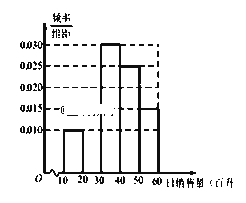
【题目】某加油站20名员工日销售量的频率分布直方图,如图所示:
(1)补全该频率分布直方图在[20,30)的部分,并分别计算日销售量在 [10,20),[20,30)的员工数;
(2)在日销量为[10,30)的员工中随机抽取2人,求这两名员工日销量在 [20,30)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com