
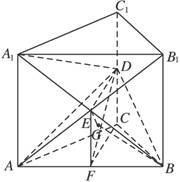
(1)求A1B与平面ABD所成角的大小(结果用反三角函数值表示);
(2)求点A1到平面AED的距离.
解法一:(1)连结BG,则BG是BE在面ABD的射影,即∠EBG是A1B与平面ABD所成的角.设F为AB的中点,连结EF、FC,

∵D、E分别是CC1、A1B的中点,
又DC⊥平面ABC,∴CDEF为矩形.
连结DF,G是△ADB的重心,
∴G∈DF.在Rt△EFD中,
EF2=FG·FD=![]() FD2,
FD2,
∵EF=1,
∴FD=![]() .
.
于是ED=![]() .
.
EG=![]() .
.
∵FC=ED=![]() ,
,
∴AB=2![]() ,A1B=2
,A1B=2![]() ,EB=
,EB=![]() .
.
∴sinEBG=![]() .
.
∴A1B与平面ABD所成的角是arcsin![]() .
.
(2)连结A1D,有![]() .
.
∵ED⊥AB,ED⊥EF.
又EF∩AB=F,
∴ED⊥平面A1AB.
设A1到平面AED的距离为h,
则S△AED·h=![]() ·ED.
·ED.
又![]() =
=![]()
![]() =
=![]() A1A·AB=
A1A·AB=![]() ,
,
S△AED=![]() AE·ED=
AE·ED=![]() .
.
∴h=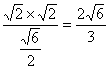 ,
,
即A1到平面AED的距离为![]() .
.
解法二:(1)连结BG,则BG是BE在面ABD上的射影,即∠A1BG是A1B与平面ABD所成的角.
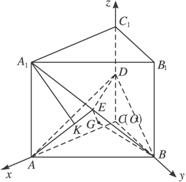
如上图所示,建立坐标系,坐标原点为O.设CA=2a,则A(2a,0,0),B(0,2a,0),?D(0,0,1),A1(2a,0,2),E(a,a,1),G(![]() ,
,![]() ,
,![]() ).
).
∴![]() =(
=(![]() ),
),![]() =(0,-2a,1).
=(0,-2a,1).
∴![]() ·
·![]() =-
=-![]() =0.解得a=1.
=0.解得a=1.
∴![]() =(2,-2,2),
=(2,-2,2),![]() =(
=(![]() ).
).
∴cosA1BG=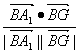 =
=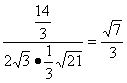 .
.
∴A1B与平面ABD所成的角是arccos![]() .
.
(2)由(1)有A(2,0,0),A1(2,0,2),E(1,1,1),D(0,0,1).
![]() =(-1,1,1)·(-1,-1,0)=0,
=(-1,1,1)·(-1,-1,0)=0,
![]() ·
·![]() =(0,0,2)·(-1,-1,0)=0,
=(0,0,2)·(-1,-1,0)=0,
∴ED⊥平面AA1E.又ED?平面AED,
∴平面AED⊥面AA1E,又面AED∩面AA1E=AE,
∴点A1在平面AED上的射影K在?AE上.
设![]() ,
,
则![]() =(-λ,λ,λ-2).
=(-λ,λ,λ-2).
由![]() =0,
=0,
即λ+λ+λ-2=0.
解得λ=![]() .
.
∴![]() =(-
=(-![]() ,
,![]() ,-
,-![]() ).
).
∴|![]() |=
|=![]() .
.
故A1到平面AED的距离为![]() .
.


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
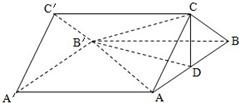 如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点.
如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数).
如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数).查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角.
如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,
如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com