【题目】已知函数
.
(1)求
的单调区间；
(2)若函数
， 
是函数
的两个零点， 
是函数
的导函数，证明： 
.
【答案】（1）见解析（2）见解析
【解析】试题分析：（1）先求函数导数，根据导函数是否变号进行讨论，当
时， 
， 
递增，当
时，导函数有一零点，导函数先正后负，故得增区间为
，减区间为
；（2）利用分析法先等价转化所证不等式：要证明
，只需证明
，即证明
，即证明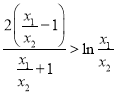
，再令
，构造函数
，利用导数研究函数
单调性，确定其最值： 
在
上递增，所以
，即可证得结论.
试题解析：(1) 
的定义域为
， 
当
时， 
， 
递增
当
时， 
递增；
递减
综上：∴当
时， 
的单调增区间为
，单调减区间为
当
时， 
的单调增区间为
（2）由
是函数
的两个零点有
，相减得
又∵
∴
所以要证明
，只需证明
即证明
，即证明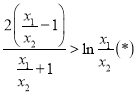
令
，则
则
， 
∴
在
上递减， 
，∴
在
上递增， 
所以
成立，即
黄冈天天练口算题卡系列答案科目：高中数学 来源： 题型：
【题目】【河南省2017届高中毕业年级考前预测数学（理）】已知圆
与直线
相切，设点
为圆上一动点， 
轴于
，且动点
满足
，设动点
的轨迹为曲线
．
（1）求曲线
的方程；
（2）直线
与直线
垂直且与曲线
交于
两点，求
面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=cos2ωx﹣sin2ωx+2 
cosωxsinωx，其中ω＞0，若f（x）相邻两条对称轴间的距离不小于 
（1）求ω的取值范围及函数f（x）的单调递增区间；
（2）在△ABC中，a，b，c分别是角A，B，C的对边，a= ，b+c=3，当ω最大时，f（A）=1，求sinBsinC的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市对贫困家庭自主创业给予小额贷款补贴，每户贷款额为
万元，贷款期限有
个月、
个月、
个月、
个月、
个月五种，这五种贷款期限政府分别需要补助
元、
元、
元、
元、
元，从
年享受此项政策的困难户中抽取了
户进行了调查统计，选取贷款期限的频数如下表：
贷款期限 |
|
|
|
|
|
频数 |
|
|
|
|
|
以商标各种贷款期限的频率作为
年贫困家庭选择各种贷款期限的概率.
（1）某小区
年共有
户准备享受此项政策，计算其中恰有两户选择贷款期限为
个月的概率；
（2）设给享受此项政策的某困难户补贴为
元，写出
的分布列，若预计
年全市有
万户享受此项政策，估计
年该市共要补贴多少万元.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}满足：a1=1，a2=2，且an+1=2an+3an﹣1（n≥2，n∈N+）．
（1）设bn=an+1+an（n∈N+），求证{bn}是等比数列；
（2）（i）求数列{an}的通项公式；
（ii）求证：对于任意n∈N+都有 
+ 
+…+ 
+ 
＜ 
成立．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】潮州统计局就某地居民的月收入调查了
人，并根据所得数据画了样本的频率分
布直方图（每个分组包括左端点，不包括右端点，如第一组表示收入在
）。
（1）求居民月收入在
的频率；
（2）根据频率分布直方图算出样本数据的中位数；
（3）为了分析居民的收入与年龄、职业等方面的关系，必须按月收入再从这人中分层抽样方法抽出
人作进一步分析，则月收入在
的这段应抽多少人？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点
，动点P 满足：|PA|=2|PB|．
(1)若点P的轨迹为曲线
，求此曲线的方程；
(2)若点Q在直线l1: x+y+3=0上，直线l2经过点Q且与曲线只有一个公共点M，求|QM|的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
