
【题目】由数列![]() 中的项构成新数列
中的项构成新数列![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…是首项为1,公比为
,…是首项为1,公比为![]() 的等比数列.
的等比数列.
(1)数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】试题分析:(1)因为新数列a1,(a2-a1),(a3-a2),…,(an-an-1),…,此数列是首项为1,公比为![]() 的等比数列,根据等比数列的通项公式可得数列{an}的通项;
的等比数列,根据等比数列的通项公式可得数列{an}的通项;
(2)通过分组分别求等差数列的和以及错位相减求和公式得到即可.
试题解析:(1)由题意知当![]() 时,
时,![]() ,
,
所以![]() ,
,
…
![]() ,
,
![]() ,
,
![]() 个式子累加得:
个式子累加得:
![]()
 ,
,
所以![]() .
.
(2)由(1)得![]() ,
,
设![]() ,
,![]() 分别为数列
分别为数列![]() ,
,![]() 的前
的前![]() 项和,
项和,
则![]() ,
,
![]() ,
,
所以![]() ,
,
两式作差得:![]()

![]() .
.
所以![]() ,
,
所以![]() .
.
点晴:本题考查的是求数列通项和数列求和问题。观察所给定数列的特征,新数列a1,(a2-a1),(a3-a2),…,(an-an-1),…,是首项为1,公比为![]() 的等比数列,根据等比数列的通项公式可得数列{an}的通项,从第二问的通项判断需要分组求和. 通过分组分别求等差数列的和以及错位相减求和公式得到即可.
的等比数列,根据等比数列的通项公式可得数列{an}的通项,从第二问的通项判断需要分组求和. 通过分组分别求等差数列的和以及错位相减求和公式得到即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.二进制数11010(2)化为八进制数为42(8)
B.若扇形圆心角为2弧度,且扇形弧所对的弦长为2,则这个扇形的面积为 ![]()
C.用秦九韶算法计算多项式f(x)=3x6+5x4+6x3﹣4x﹣5当x=3时的值时,v1=3v0+5=32
D.正切函数在定义域内为单调增函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
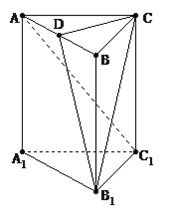
【题目】如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC, 点D是AB的中点.
(Ⅰ)求证:CD⊥平面A1ABB1;
(Ⅱ)求证:AC1∥平面CDB1;
(Ⅲ)线段AB上是否存在点M,使得A1M⊥平面CDB1?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 与圆
与圆![]() :
: ![]() 相切,且与圆
相切,且与圆![]() :
: ![]() 相内切,记圆心
相内切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .设
.设![]() 为曲线
为曲线![]() 上的一个不在
上的一个不在![]() 轴上的动点,
轴上的动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交曲线
的平行线交曲线![]() 于
于![]() ,
, ![]() 两个不同的点.
两个不同的点.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)试探究![]() 和
和![]() 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
(Ⅲ)记![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四边形ABCD中,已知AB=9,BC=6, ![]() =2
=2 ![]() .
.
(1)若四边形ABCD是矩形,求 ![]()
![]() 的值;
的值;
(2)若四边形ABCD是平行四边形,且 ![]()
![]() =6,求
=6,求 ![]() 与
与 ![]() 夹角的余弦值.
夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
![]()
| 应该取消 | 应该保留 | 无所谓 | |
在校学生 | 2100人 | 120人 | y人 | |
社会人士 | 600人 | x人 | z人 |
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.05.
(1)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
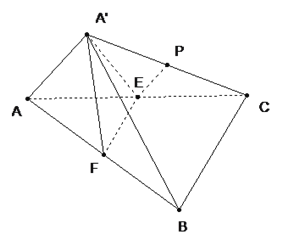
【题目】如图, ![]() 、
、![]() 分别为直角三角形
分别为直角三角形![]() 的直角边
的直角边![]() 和斜边
和斜边![]() 的中点,沿
的中点,沿![]() 将
将![]() 折起到
折起到![]() 的位置,连结
的位置,连结![]() 、
、![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;(2)求证:平面
;(2)求证:平面![]() 平面
平面![]() ;
;
(3)求证: ![]() 平面
平面![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com