
【题目】如图,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,D为AC上一点,将
,D为AC上一点,将![]() 沿BD折起,得到三棱锥
沿BD折起,得到三棱锥![]() ,且使得
,且使得![]() 在底面BCD的投影E在线段BC上,连接AE.
在底面BCD的投影E在线段BC上,连接AE.
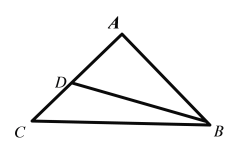
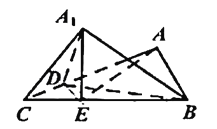
(1)证明:![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】对于数列![]() 、
、![]() ,把和
,把和![]() 叫做数列
叫做数列![]() 与
与![]() 的前
的前![]() 项泛和,记作为
项泛和,记作为![]() .已知数列
.已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 与数列
与数列![]() 的前
的前![]() 项的泛和为
项的泛和为![]() ,且
,且![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)从数列![]() 的前
的前![]() 项中,任取
项中,任取![]() 项从小到大依次排列,得到数列
项从小到大依次排列,得到数列![]() 、
、![]() 、
、![]() 、
、![]() ;再将余下的
;再将余下的![]() 项从大到小依次排列,得到数列
项从大到小依次排列,得到数列![]() 、
、![]() 、
、![]() 、
、![]() .求数列
.求数列![]() 与数列
与数列![]() 的前
的前![]() 项的泛和
项的泛和![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E为D1D的中点,AC与BD的交点为O.
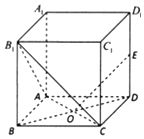
(1)求证:EO⊥平面AB1C;
(2)在由正方体的顶点确定的平面中,是否存在与平面AB1C平行的平面?证明你的结论
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() ,给出下列命题:
,给出下列命题:
①当![]() 时,
时,![]() ;
;
②函数![]() 有2个零点;
有2个零点;
③![]() 的解集为
的解集为![]() ;
;
④![]() ,
,![]() ,都有
,都有![]() .
.
其中真命题的个数为( )
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车的投放,方便了市民短途出行,被誉为中国“新四大发明”之一.某市为研究单车用户与年龄的相关程度,随机调查了100位成人市民,统计数据如下:
不小于40岁 | 小于40岁 | 合计 | |
单车用户 | 12 | 18 | 30 |
非单车用户 | 38 | 32 | 70 |
合计 | 50 | 50 | 100 |
(1)从独立性检验角度分析,能否有![]() 以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关;
以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关;
(2)将此样本的频率做为概率,从该市单车用户中随机抽取3人,记不小于40岁的单车用户的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
下面临界值表供参考:
P( | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: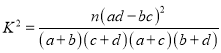 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,有下列四个命题:
,有下列四个命题:
①函数![]() 是奇函数;
是奇函数;
②函数![]() 在
在![]() 是单调函数;
是单调函数;
③当![]() 时,函数
时,函数![]() 恒成立;
恒成立;
④当![]() 时,函数
时,函数![]() 有一个零点,
有一个零点,
其中正确的是____________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,然后纵坐标不变,横坐标变为原来的
个单位,然后纵坐标不变,横坐标变为原来的![]() 倍,得到
倍,得到![]() 的图象,下面四个结论正确的是( )
的图象,下面四个结论正确的是( )
A. 函数![]() 在区间
在区间![]() 上为增函数
上为增函数
B. 将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后得到的图象关于原点对称
个单位后得到的图象关于原点对称
C. 点![]() 是函数
是函数![]() 图象的一个对称中心
图象的一个对称中心
D. 函数![]() 在
在![]() 上的最大值为
上的最大值为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com