
【题目】已知函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() ,给出下列命题:
,给出下列命题:
①当![]() 时,
时,![]() ;
;
②函数![]() 有2个零点;
有2个零点;
③![]() 的解集为
的解集为![]() ;
;
④![]() ,
,![]() ,都有
,都有![]() .
.
其中真命题的个数为( )
A.4B.3C.2D.1
【答案】C
【解析】
对于①,利用函数![]() 是定义在R上的奇函数求解即可;对于②,由函数解析式及函数为奇函数求解即可;对于③,分别解当
是定义在R上的奇函数求解即可;对于②,由函数解析式及函数为奇函数求解即可;对于③,分别解当![]() 时,当
时,当![]() 时,
时,![]() 即可得解;对于④,利用导数研究函数的单调性,再求值域即可得解.
即可得解;对于④,利用导数研究函数的单调性,再求值域即可得解.
解:对于①,函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() ,则当
,则当![]() 时,
时,![]()
![]() ,即①错误;
,即①错误;
对于②,由题意可得![]() ,即函数
,即函数![]() 有3个零点,即②错误;
有3个零点,即②错误;
对于③,当![]() 时,
时,![]() ,令
,令![]() ,解得
,解得![]() ,当
,当![]() 时,
时,![]()
![]() ,令
,令![]() ,解得
,解得![]() ,综上可得
,综上可得![]() 的解集为
的解集为![]() ,即③正确;
,即③正确;
对于④,当![]() 时,
时,![]() ,
,![]() ,令
,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,即函数
,即函数![]() 在
在![]() 为减函数,在
为减函数,在![]() 为增函数,即函数在
为增函数,即函数在![]() 的最小值为
的最小值为![]() ,且
,且![]() 时,
时,![]() ,又
,又![]() ,则
,则![]() ,由函数为奇函数可得当
,由函数为奇函数可得当![]() 时,
时,![]() ,又
,又![]() ,即函数
,即函数![]() 的值域为
的值域为![]() ,即
,即![]() ,
,![]() ,都有
,都有![]() ,即④正确,
,即④正确,
即真命题的个数为2,
故选:C.


科目:高中数学 来源: 题型:
【题目】某客户考察了一款热销的净水器,使用寿命为十年,过滤由核心部件滤芯来实现.在使用过程中,滤芯需要不定期更换,其中滤芯每个200元.如图是根据100台该款净水器在十年使用期内更换的滤芯的件数制成的柱状图.(以100台净水器更换滤芯的频率代替1台净水器更换滤芯发生的概率)
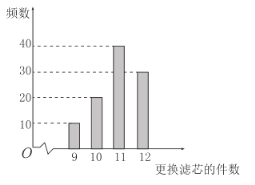
(1)估计一台净水器在使用期内更换滤芯的件数的众数和中位数.
(2)估计一台净水器在使用期内更换滤芯的件数大于10的概率.
(3)已知上述100台净水器在购机的同时购买滤芯享受5折优惠(使用过程中如需再购买无优惠),假设每台净水器在购机的同时购买滤芯10个,这100台净水器在使用期内,更换滤芯的件数记为a,所需费用记为y,补全下表,估计这100台净水器在使用期内购买滤芯所需总费用的平均数.
100台该款净水器在试用期内更换滤芯的件数a | 9 | 10 | 11 | 12 |
频数 | ||||
费用y |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 、
、![]() ,线段
,线段![]() 的长为4.点
的长为4.点![]() 在椭圆
在椭圆![]() 上且位于第一象限,过点
上且位于第一象限,过点![]() ,
,![]() 分别作
分别作![]() ,
,![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
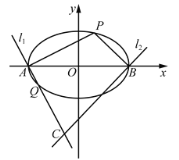
(1)若点![]() 的横坐标为-1,求点
的横坐标为-1,求点![]() 的坐标;
的坐标;
(2)直线![]() 与椭圆
与椭圆![]() 的另一交点为
的另一交点为![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() ,给出下列命题:
,给出下列命题:
①当![]() 时,
时,![]() ;
;
②函数![]() 有2个零点;
有2个零点;
③![]() 的解集为
的解集为![]() ;
;
④![]() ,
,![]() ,都有
,都有![]() .
.
其中真命题的个数为( )
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
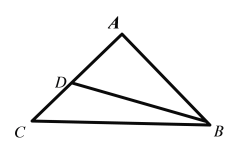
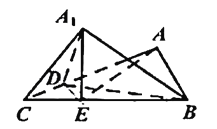
【题目】如图,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,D为AC上一点,将
,D为AC上一点,将![]() 沿BD折起,得到三棱锥
沿BD折起,得到三棱锥![]() ,且使得
,且使得![]() 在底面BCD的投影E在线段BC上,连接AE.
在底面BCD的投影E在线段BC上,连接AE.
(1)证明:![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若对任意的实数k,b,函数![]() 与直线
与直线![]() 总相切,则称函数
总相切,则称函数![]() 为“恒切函数”.
为“恒切函数”.
(1)判断函数![]() 是否为“恒切函数”;
是否为“恒切函数”;
(2)若函数![]() 是“恒切函数”,求实数m,n满足的关系式;
是“恒切函数”,求实数m,n满足的关系式;
(3)若函数![]() 是“恒切函数”,求证:
是“恒切函数”,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com