
【题目】已知椭圆![]() :
:![]() (
(![]() )过点
)过点![]() 与
与![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过椭圆![]() 的右焦点
的右焦点![]() ,且倾斜角为
,且倾斜角为![]() 的直线
的直线![]() 和椭圆
和椭圆![]() 交于
交于![]() 、
、![]() 两点,对于椭圆
两点,对于椭圆![]() 上任一点
上任一点![]() ,若
,若![]() ,求
,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得![]() 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm2
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm2
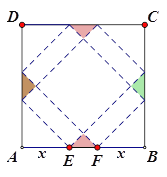
(1)若广告商要求包装盒侧面积S(cm![]() )最大,试问x应取何值?
)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm![]() )最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】谢宾斯基三角形是一种分形,由波兰数学家谢宾斯基在1915年提出,先作一个正三角形.挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的小三角形中又挖去一个“中心三角形”,我们用白色代表挖去的面积,那么黑三角形为剩下的面积(我们称黑三角形为谢宾斯基三角形).向图中第5个大正三角形中随机撒512粒大小均匀的细小颗粒物,则落在白色区域的细小颗粒物的数量约是( )

A.256B.350C.162D.96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() 、
、![]() ,把和
,把和![]() 叫做数列
叫做数列![]() 与
与![]() 的前
的前![]() 项泛和,记作为
项泛和,记作为![]() .已知数列
.已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 与数列
与数列![]() 的前
的前![]() 项的泛和为
项的泛和为![]() ,且
,且![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)从数列![]() 的前
的前![]() 项中,任取
项中,任取![]() 项从小到大依次排列,得到数列
项从小到大依次排列,得到数列![]() 、
、![]() 、
、![]() 、
、![]() ;再将余下的
;再将余下的![]() 项从大到小依次排列,得到数列
项从大到小依次排列,得到数列![]() 、
、![]() 、
、![]() 、
、![]() .求数列
.求数列![]() 与数列
与数列![]() 的前
的前![]() 项的泛和
项的泛和![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() ,给出下列命题:
,给出下列命题:
①当![]() 时,
时,![]() ;
;
②函数![]() 有2个零点;
有2个零点;
③![]() 的解集为
的解集为![]() ;
;
④![]() ,
,![]() ,都有
,都有![]() .
.
其中真命题的个数为( )
A.4B.3C.2D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com