
【题目】请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得![]() 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm2
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm2
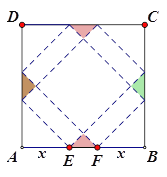
(1)若广告商要求包装盒侧面积S(cm![]() )最大,试问x应取何值?
)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm![]() )最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
科目:高中数学 来源: 题型:
【题目】为了了解市民对开设传统文化课的态度,教育机构随机抽取了![]() 位市民进行了解,发现支持开展的占
位市民进行了解,发现支持开展的占![]() ,在抽取的男性市民
,在抽取的男性市民![]() 人中持支持态度的为
人中持支持态度的为![]() 人.
人.
(1)完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为性别与支持与否有关?
的把握认为性别与支持与否有关?
支持 | 不支持 | 合计 | |
男性 | |||
女性 | |||
合计 |
(2)为了进一步征求对开展传统文化的意见和建议,从抽取的![]() 位市民中对不支持的按照分层抽样的方法抽取
位市民中对不支持的按照分层抽样的方法抽取![]() 位市民,并从抽取的
位市民,并从抽取的![]() 人中再随机选取
人中再随机选取![]() 人进行座谈,求选取的
人进行座谈,求选取的![]() 人恰好为
人恰好为![]() 男
男![]() 女的概率.
女的概率.
附: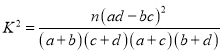
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]()
![]() 在椭圆
在椭圆![]()
![]() 上,且椭圆的离心率为
上,且椭圆的离心率为![]() .
.
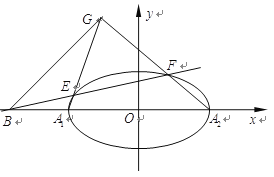
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)记椭圆的左、右顶点分别为![]() ,过点
,过点![]() 或
或![]() 作一条直线交椭圆
作一条直线交椭圆![]() 于
于![]() 、
、![]() (不与
(不与![]() 重合)两点,直线
重合)两点,直线![]() 交于点
交于点![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .
.
①对于给定的![]() ,求
,求![]() 的值;
的值;
②是否存在一个定值![]() 使得
使得![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为了调查该校学生性别与身高的关系,对该校1000名学生按照![]() 的比例进行抽样调查,得到身高频数分布表如下:
的比例进行抽样调查,得到身高频数分布表如下:
男生身高频率分布表
男生身高 (单位:厘米) |
|
|
|
|
|
|
频数 | 7 | 10 | 19 | 18 | 4 | 2 |
女生身高频数分布表
女生身高 (单位:厘米) |
|
|
|
|
|
|
频数 | 3 | 10 | 15 | 6 | 3 | 3 |
(1)估计这1000名学生中女生的人数;
(2)估计这1000名学生中身高在![]() 的概率;
的概率;
(3)在样本中,从身高在![]() 的女生中任取2名女生进行调查,求这2名学生身高在
的女生中任取2名女生进行调查,求这2名学生身高在![]() 的概率.(身高单位:厘米)
的概率.(身高单位:厘米)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车又称为小黄车,近年来逐渐走进了人们的生活,也成为减少空气污染,缓解城市交通压力的一种重要手段.为调查某地区居民对共享单车的使用情况,从该地区居民中按年龄用随机抽样的方式随机抽取了![]() 人进行问卷调查,得到这
人进行问卷调查,得到这![]() 人对共享单车的评价得分统计填入茎叶图,如下所示(满分
人对共享单车的评价得分统计填入茎叶图,如下所示(满分![]() 分):
分):

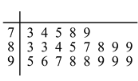
(1)找出居民问卷得分的众数和中位数;
(2)请计算这![]() 位居民问卷的平均得分;
位居民问卷的平均得分;
(3)若在成绩为![]() 分的居民中随机抽取
分的居民中随机抽取![]() 人,求恰有
人,求恰有![]() 人成绩超过
人成绩超过![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为![]() 的正方形中
的正方形中![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,沿
的中点,沿![]() 将矩形
将矩形![]() 折起使得
折起使得![]() ,如图2所示,点
,如图2所示,点![]() 在
在![]() 上,
上,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点.
中点.
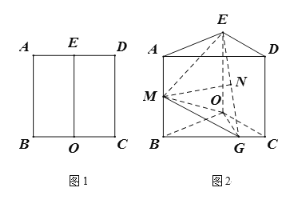
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com