
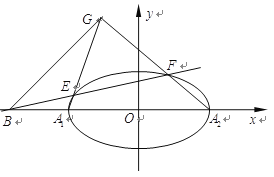
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]()
![]() 在椭圆
在椭圆![]()
![]() 上,且椭圆的离心率为
上,且椭圆的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)记椭圆的左、右顶点分别为![]() ,过点
,过点![]() 或
或![]() 作一条直线交椭圆
作一条直线交椭圆![]() 于
于![]() 、
、![]() (不与
(不与![]() 重合)两点,直线
重合)两点,直线![]() 交于点
交于点![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .
.
①对于给定的![]() ,求
,求![]() 的值;
的值;
②是否存在一个定值![]() 使得
使得![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②存在,
;②存在,![]() .
.
【解析】
(1)结合点在椭圆上和椭圆的离心率可解得![]() ,
,![]() ,进而写出椭圆的标准方程;
,进而写出椭圆的标准方程;
(2)①利用点斜式写出直线![]() 和
和![]() 的方程分别为
的方程分别为![]() 和
和![]() ,再分别与椭圆联立,结合韦达定理,可求得
,再分别与椭圆联立,结合韦达定理,可求得![]() ,
,![]() ,然后利用
,然后利用![]() 、
、![]() 、
、![]() 三点共线时,任意两点构成的直线斜率相等来构造等式即可得解,需要注意的是验证
三点共线时,任意两点构成的直线斜率相等来构造等式即可得解,需要注意的是验证![]() 不符合题意;
不符合题意;
②联立直线![]() 和
和![]() 的方程可解得点
的方程可解得点![]() ,再利用
,再利用![]() 、
、![]() 两点的坐标表示出直线
两点的坐标表示出直线![]() 的斜率
的斜率![]() ,然后结合①中得到的结论,计算化简可得到
,然后结合①中得到的结论,计算化简可得到![]() ,进而得解.
,进而得解.
(1)根据题意![]() ,离心率
,离心率![]() ,解得
,解得![]() ,
,![]() ,
,
所以椭圆![]() 的标准方程
的标准方程![]() ;
;
(2)①因为椭圆的左、右顶点分别为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
因为直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,所以直线
,所以直线![]() 和
和![]() 的方程分别为
的方程分别为![]() 和
和![]() ,
,
设![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
联立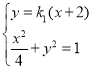 得,
得,![]() ,
,
则![]() ,即
,即![]() ,
,
解得![]() ,
,![]() ,所以
,所以![]() .
.
同理可得,点![]() 的坐标为
的坐标为![]() .
.
因为![]() 、
、![]() 、
、![]() 三点共线,所以
三点共线,所以![]() ,即
,即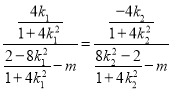 ,
,
化简得![]() .
.
所以![]() 或
或![]() ,即
,即![]() 或
或![]() .
.
当![]() 时,此时点
时,此时点![]() 位于椭圆的上或下顶点,即
位于椭圆的上或下顶点,即![]() 、
、![]() 分别与
分别与![]() ,
,![]() 重合,与题干矛盾,故舍去.
重合,与题干矛盾,故舍去.
综上,对于给定的![]() ,
,![]() .
.
②由①知直线![]() 和
和![]() 的方程分别为
的方程分别为![]() 和
和![]() ,
,
联立可解得点![]() 的坐标为
的坐标为![]() ,
,
因为点![]() ,所以
,所以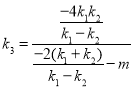 ,
,
化简得![]() ,
,
由①的结论可知![]() ,所以
,所以![]() ,将其代入上式,
,将其代入上式,
化简整理后可得,![]() ,
,
故存在定值![]() 使得
使得![]() 恒成立,且
恒成立,且![]() .
.


科目:高中数学 来源: 题型:
【题目】某大型超市抽查了100天该超市的日纯利润数据,并将日纯利润数据分成以下几组(单位:万元):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,统计结果如下表所示:
,统计结果如下表所示:
组别 |
|
|
|
|
|
|
频数 | 5 | 20 | 30 | 30 | 10 | 5 |
以上述样本分布的频率估计总体分布的概率,解决下列问题:
(1)从该大型超市近几年的销售记录中抽出5天,求其中日纯利润在区间![]() 内的天数不少于2的概率;
内的天数不少于2的概率;
(2)该超市经理由频数分布表可以认为,该大型超市每天的纯利润![]() 服从正态分布
服从正态分布![]() ,其中,
,其中,![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值).
(每组数据取区间的中点值).
①试利用该正态分布,估计该大型超市1000天内日纯利润在区间![]() 内的天数(精确到个位);
内的天数(精确到个位);
②该大型超市负责人根据每日的纯利润给超市员工制定了两种不同的奖励方案:
方案一:直接发放奖金,日纯利润低于![]() 时每名员工发放奖金70元,日纯利润不低于
时每名员工发放奖金70元,日纯利润不低于![]() 时每名员工发放奖金90元;
时每名员工发放奖金90元;
方案二:利用抽奖的方式获得奖金,其中日纯利润不低于![]() 时每位员工均有两次抽奖机会,日纯利润低于
时每位员工均有两次抽奖机会,日纯利润低于![]() 时每位员工只有一次抽奖机会;每次抽奖的奖金及对应的概率分别为
时每位员工只有一次抽奖机会;每次抽奖的奖金及对应的概率分别为
金额 | 50元 | 100元 |
概率 |
|
|
小张恰好为该大型超市的一名员工,则从数学期望的角度看,小张选择哪种奖励方案更有利?
参考数据:若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的产品中分正品与次品,正品重![]() ,次品重
,次品重![]() ,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第
,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第![]() 袋取出
袋取出![]() 个产品(
个产品(![]() ),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量
),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量![]() ,若次品所在的袋子的编号是2,此时的重量
,若次品所在的袋子的编号是2,此时的重量![]() _________
_________![]() ;若次品所在的袋子的编号是
;若次品所在的袋子的编号是![]() ,此时的重量
,此时的重量![]() _______
_______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】奇函数f(x)在R上存在导数![]() ,当x<0时,
,当x<0时,![]()
![]() f(x),则使得(x2﹣1)f(x)<0成立的x的取值范围为( )
f(x),则使得(x2﹣1)f(x)<0成立的x的取值范围为( )
A.(﹣1,0)∪(0,1)B.(﹣∞,﹣1)∪(0,1)
C.(﹣1,0)∪(1,+∞)D.(﹣∞,﹣1)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
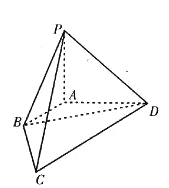
【题目】如图,在四棱锥![]() 中,已知棱
中,已知棱![]() ,
,![]() ,
,![]() 两两垂直,长度分别为1,2,2.若
两两垂直,长度分别为1,2,2.若![]() (
(![]() ),且向量
),且向量![]() 与
与![]() 夹角的余弦值为
夹角的余弦值为![]() .
.
(1)求![]() 的值;
的值;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周率是圆的周长与直径的比值,一般用希腊字母![]() 表示.早在公元480年左右,南北朝时期的数学家祖冲之就得出精确到小数点后7位的结果,他是世界上第一个把圆周率的数值计算到小数点后第7位的人,这比欧洲早了约1000年.生活中,我们也可以通过如下随机模拟试验来估计
表示.早在公元480年左右,南北朝时期的数学家祖冲之就得出精确到小数点后7位的结果,他是世界上第一个把圆周率的数值计算到小数点后第7位的人,这比欧洲早了约1000年.生活中,我们也可以通过如下随机模拟试验来估计![]() 的值:在区间
的值:在区间![]() 内随机取
内随机取![]() 个数,构成
个数,构成![]() 个数对
个数对![]() ,设
,设![]() ,
,![]() 能与1构成钝角三角形三边的数对
能与1构成钝角三角形三边的数对![]() 有
有![]() 对,则通过随机模拟的方法得到的
对,则通过随机模拟的方法得到的![]() 的近似值为( )
的近似值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
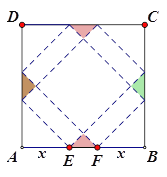
【题目】请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得![]() 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm2
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm2
(1)若广告商要求包装盒侧面积S(cm![]() )最大,试问x应取何值?
)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm![]() )最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把编号为1,2,3,4,5的五个大小、形状相同的小球,随机放入编号为1,2,3,4,5的五个盒子里.每个盒子里放入一个小球.
(1)求恰有两个球的编号与盒子的编号相同的概率;
(2)设恰有![]() 个小球的编号与盒子编号相同,求随机变量
个小球的编号与盒子编号相同,求随机变量![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com