
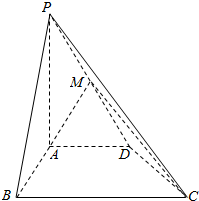
 如图在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点.
如图在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点.分析 (1)以A为原点,过A作BC的垂线为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法得到$\overrightarrow{AP}⊥\overrightarrow{AC}$,$\overrightarrow{AB}⊥\overrightarrow{AC}$,由此能证明平面AMC⊥平面PAB.
(2)求出平面ABM的法向量和平面ABC的法向量,利用向量法能求出二面角M-AB-C的余弦值.
解答 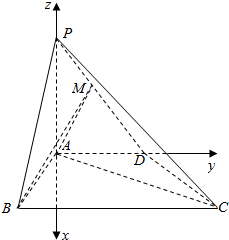 (1)证明:以A为原点,过A作BC的垂线为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
(1)证明:以A为原点,过A作BC的垂线为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
由已知得A(0,0,0),P(0,0,4),B($\sqrt{3}$,-1,0),C($\sqrt{3}$,3,0),
∴$\overrightarrow{AP}$=(0,0,4),$\overrightarrow{AB}$=($\sqrt{3},-1,0$),$\overrightarrow{AC}$=($\sqrt{3},3,0$),
∴$\overrightarrow{AP}•\overrightarrow{AC}$=0,$\overrightarrow{AB}•\overrightarrow{AC}$=3-3+0=0,
∴$\overrightarrow{AP}⊥\overrightarrow{AC}$,$\overrightarrow{AB}⊥\overrightarrow{AC}$,∴AP⊥AC,AB⊥AC,
∵AB∩AP=P,∴AC⊥平面PAB,
∵AC?平面AMC,∴平面AMC⊥平面PAB.
(2)解:D(0,2,0),M(0,1,2),$\overrightarrow{AB}$=($\sqrt{3},-1,0$),$\overrightarrow{AM}$=(0,1,2),
设平面ABM的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=\sqrt{3}x-y=0}\\{\overrightarrow{n}•\overrightarrow{AM}=y+2z=0}\end{array}\right.$,取x=$\sqrt{3}$,得$\overrightarrow{n}$=($\sqrt{3},3,-\frac{3}{2}$),
又平面ABC的法向量$\overrightarrow{m}$=(0,0,1),
设二面角M-AB-C的平面角为θ,
则cosθ=|cos<$\overrightarrow{n},\overrightarrow{m}$>|=|$\frac{\overrightarrow{n}•\overrightarrow{m}}{|\overrightarrow{n}|•|\overrightarrow{m}|}$|=|$\frac{-\frac{3}{2}}{\frac{\sqrt{57}}{2}}$|=$\frac{3\sqrt{57}}{57}$=$\frac{\sqrt{57}}{19}$.
∴二面角M-AB-C的余弦值为$\frac{\sqrt{57}}{19}$.
点评 本题考查面面垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,±$\sqrt{12-2k}$) | B. | (±$\sqrt{12-2k}$,0) | C. | (0,±2) | D. | (±2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “所有金属都能导电,铁是金属,所以铁能导电”这种推理属于演绎推理 | |
| B. | 已知数据x1,x2,…,xn的方差是4,则数据-3x1+2015,-3x2+2015,…,-3xn+2015的标准差是6 | |
| C. | 用相关指数R2来刻画回归效果,R2的值越小,说明模型的拟合效果越好 | |
| D. | 若变量y和x之间的相关系数r=-0.9362,则变量y和x之间具有很强的线性相关关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在棱柱ABC-A1B1C1中,底面为正三角形,侧棱长等于底面边长,且侧棱与底面所成的角为60°,顶点为B1在底面ABC上的射影O恰好是AB的中点
如图,在棱柱ABC-A1B1C1中,底面为正三角形,侧棱长等于底面边长,且侧棱与底面所成的角为60°,顶点为B1在底面ABC上的射影O恰好是AB的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com