
| A. | (0,±$\sqrt{12-2k}$) | B. | (±$\sqrt{12-2k}$,0) | C. | (0,±2) | D. | (±2,0) |
分析 双曲线$\frac{{x}^{2}}{8-k}$+$\frac{{y}^{2}}{4-k}$=1可化为$\frac{{x}^{2}}{8-k}$-$\frac{{y}^{2}}{k-4}$=1,即可求出双曲线$\frac{{x}^{2}}{8-k}$+$\frac{{y}^{2}}{4-k}$=1的焦点坐标.
解答 解:双曲线$\frac{{x}^{2}}{8-k}$+$\frac{{y}^{2}}{4-k}$=1可化为$\frac{{x}^{2}}{8-k}$-$\frac{{y}^{2}}{k-4}$=1,
∴c=$\sqrt{8-k+k-4}$=2,
∴双曲线$\frac{{x}^{2}}{8-k}$+$\frac{{y}^{2}}{4-k}$=1的焦点坐标是(±2,0).
故选:D.
点评 本题考查双曲线的性质,考查学生的计算能力,比较基础.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:解答题
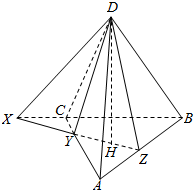 过正四面体ABCD的高DH作一平面,与正四面体的三个侧面相交得到三条直线DX,DY,DZ,这三条直线与正四面体的底面所成角分别为$\alpha$,$\beta$,$\gamma$.求证:tan2α+tan2β+tan2γ=12.
过正四面体ABCD的高DH作一平面,与正四面体的三个侧面相交得到三条直线DX,DY,DZ,这三条直线与正四面体的底面所成角分别为$\alpha$,$\beta$,$\gamma$.求证:tan2α+tan2β+tan2γ=12.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
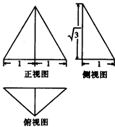
| A. | $\frac{{\sqrt{3}}}{3}π$ | B. | $\frac{16}{3}π$ | C. | $\frac{26}{3}π$ | D. | $\frac{{32\sqrt{3}}}{27}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
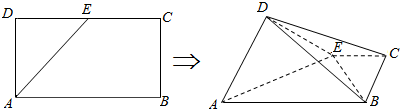
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
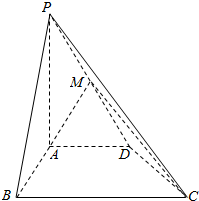 如图在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点.
如图在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
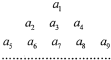 已知an=($\frac{1}{3}$)n,把数列{an}的各项排列成如下的三角形状:记A(m,n)表示第m行的第n个数,则A(11,2)( )
已知an=($\frac{1}{3}$)n,把数列{an}的各项排列成如下的三角形状:记A(m,n)表示第m行的第n个数,则A(11,2)( )| A. | ($\frac{1}{3}$)67 | B. | ($\frac{1}{3}$)68 | C. | ($\frac{1}{3}$)101 | D. | ($\frac{1}{3}$)102 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com