
分析 由题意画出图形,令$\overrightarrow{OA}=\overrightarrow{m},\overrightarrow{OB}=\overrightarrow{n}$,然后把$\overrightarrow{AB}、\overrightarrow{BC}$用向量$\overrightarrow{m}、\overrightarrow{n}$表示,由数量积运算证明$\overrightarrow{AB}•\overrightarrow{BC}=0$得答案.
解答 证明:如图,
设圆O半径为r,令$\overrightarrow{OA}=\overrightarrow{m},\overrightarrow{OB}=\overrightarrow{n}$,
则$\overrightarrow{OC}=-\overline{m}$,且$|\overrightarrow{m}|=|\overrightarrow{n}|=r$
∴$\overrightarrow{AB}•\overrightarrow{BC}=(\overrightarrow{OB}-\overrightarrow{OA})•(\overrightarrow{OC}-\overrightarrow{OB})$
=$(\overrightarrow{n}-\overrightarrow{m})•(-\overrightarrow{m}-\overrightarrow{n})$=$(\overrightarrow{m})^{2}-(\overrightarrow{n})^{2}=|\overrightarrow{m}{|}^{2}-|\overrightarrow{n}{|}^{2}={r}^{2}-{r}^{2}=0$.
∴$\overrightarrow{AB}⊥\overrightarrow{BC}$.
即AB⊥BC.
∴∠ABC=90°.
点评 本题考查平面向量数量积的运算,训练了平面向量的加减法运算,是基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
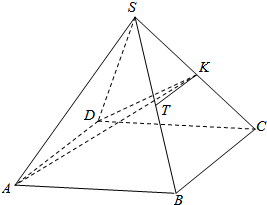 如图,正四棱锥S-ABCD中,底面边长与高相等,K、T分别是SC、SB的中点.
如图,正四棱锥S-ABCD中,底面边长与高相等,K、T分别是SC、SB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在正方形ABCD-A1B1C1D1中:
如图所示,在正方形ABCD-A1B1C1D1中:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,±$\sqrt{12-2k}$) | B. | (±$\sqrt{12-2k}$,0) | C. | (0,±2) | D. | (±2,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com