
����Ŀ��ijУ��һ�꼶ij����ѧ���������ȡ100��ѧ���ijɼ�������Ϊ[50��60����[60��70����[70��80����[80��90����[90��100]��ͳ�ƺ�õ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��

��1���Թ��������������ݵ���������λ���������ȷ��0.1����
��2���꼶�����ڳɼ�[70��100]���÷ֲ������ȡ6�����һ������С�飬�Ը�һ�꼶ѧ������ѧϰ��ѧ�������һ�����飬����[70��80����[80��90����[90��100]������ֱ��ȡ�˶����ˣ�
��3������Ҫ�ӣ�2���г�ȡ��6����ѡ������2��С�鳤����ɼ���[80��90����������1�˵�ѡΪ������С�鳤�ĸ��ʣ�
���𰸡���1��65��73.3����2��3��2��1����3��![]()
�������������������1����Ƶ�ʷֲ�ֱ��ͼ��������ľ����е�ɵ����������������Ϊ0.5�ķֽ紦Ϊ��λ����
��2��������ɼ�Ϊ[70��80����[80��90����[90��100]�������Ƶ�ʣ��ɴ������[70��80����[80��90����[90��100]�������ȡ��������
��3���ɣ�2��֪�ɼ���[70��80����3�ˣ��ֱ��Ϊa��b��c���ɼ���[80��90����2�ˣ��ֱ��Ϊd��e���ɼ���[90��100]��1�ˣ���Ϊf���ɴ������оٷ�������ɼ���[80��90����������1�˵�ѡΪ������С�鳤�ĸ��ʣ�
���������
��1����Ƶ�ʷֲ�ֱ��ͼ�ã�����Ϊ��![]() =65��
=65��
�ɼ���[50��70���ڵ�Ƶ��Ϊ����0.005+0.035����10=0.4��
�ɼ���[70��80���ڵ�Ƶ��Ϊ��0.03��10=0.3��
�������70+![]() ��10��73.3��
��10��73.3��
��2���ɼ�Ϊ[70��80����[80��90����[90��100]�������Ƶ�ʷֱ�Ϊ0.3��0.2��0.1��
��[70��80����[80��90����[90��100]�������ȡ�������ֱ�Ϊ3�ˣ�2�ˣ�1�ˣ�
��3���ɣ�2��֪�ɼ���[70��80����3�ˣ��ֱ��Ϊa��b��c��
�ɼ���[80��90����2�ˣ��ֱ��Ϊd��e���ɼ���[90��100]��1�ˣ���Ϊf��
���ӣ�2���г�ȡ��6����ѡ������2��С�鳤�����Ļ����¼���![]() �֣��ֱ�Ϊ��
�֣��ֱ�Ϊ��
ab��ba��ac��ca��ad��da��ae��ea��af��fa��bc��cb��bd��db��be��eb��bf��fb��cd��dc��ce��ec��cf��fc��de��ed��df��fd��ef��fe��
�ǡ��ɼ���[80��90����������1�˵�ѡΪ������С�鳤��Ϊ�¼�Q��
���¼�Q�����Ļ����¼���18�֣�
���ɼ���[80��90����������1�˵�ѡΪ������С�鳤�ĸ���P��Q��=![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ǹ���
�ǹ���![]() ��ż����.
��ż����.
(1)��![]() ��ֵ��
��ֵ��
(2)��֤: ������ʵ��![]() ������
������![]() ��ͼ���뺯��
��ͼ���뺯��![]() ��ͼ�����ֻ��һ������.
��ͼ�����ֻ��һ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �ĶԽ���
�ĶԽ���![]() ��
��![]() �ཻ��
�ཻ��![]() �㣬��
�㣬��![]() �ضԽ�������ʹ��ƽ��
�ضԽ�������ʹ��ƽ��![]() ƽ��
ƽ��![]() ����ͼ������������������ȷ������ ��
����ͼ������������������ȷ������ ��
A. ֱ��![]() ֱ��
ֱ��![]() ����ֱ��
����ֱ��![]() ֱ��
ֱ��![]()
B. ֱ��![]() ƽ��
ƽ��![]() ����ֱ��
����ֱ��![]() ƽ��
ƽ��![]()
C. ƽ��![]() ƽ��
ƽ��![]() ����ƽ��
����ƽ��![]() ƽ��
ƽ��![]()
D. ƽ��![]() ƽ��
ƽ��![]() ����ƽ��
����ƽ��![]() ƽ��
ƽ��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����봨��������Ƽ�ɽ�����������չ����У��侯�ٱ���������ķ��������Ӻ�������Ư�����µ�һ��������ޣ���ֻ֪��5���ӵ�����һ������ֻ��ʹ�����������ڶ������в���������ÿ�������������ģ������еĸ��ʶ��� ![]() ��
��
��1�����ޱ������ĸ��ʣ�
��2������������ӵ������ֹͣ��������������Ϊ�Σ���εķֲ��м���ѧ����E���Σ����� ����÷�����ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ��ֱ��y=
��ֱ��y= ![]() xΪ����y=f��x�������ߣ�eΪ��Ȼ�����ĵ�������
xΪ����y=f��x�������ߣ�eΪ��Ȼ�����ĵ�������
��1����ʵ��a��ֵ��
��2����min{m��n}��ʾm��n�е���Сֵ���躯��g��x��=min{f��x����x�� ![]() }��x��0����������h��x��=g��x����cx2Ϊ����������ʵ��c��ȡֵ��Χ��
}��x��0����������h��x��=g��x����cx2Ϊ����������ʵ��c��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
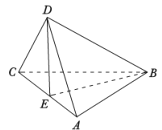
����Ŀ��������P��ABCD�У�����ABCD��һֱ�����Σ�BA��AD��AD��BC��AB=BC=2��PA=3��PA�͵���ABCD��E����PD������P��D�Ķ��㣮�� ![]() =m����0��m��2��������C��ABE�������С��1�ģ� ��
=m����0��m��2��������C��ABE�������С��1�ģ� �� 
A.��ֲ���Ҫ����
B.��Ҫ���������
C.��Ҫ����
D.�Ȳ����Ҳ����Ҫ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��0��a��1��������f��x��=loga[ax2����2��a��x+3]��[ ![]() ��2]��������������a��ȡֵ��Χ�� ��
��2]��������������a��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�뾶�ֱ�Ϊ R ��r ������Բ�����ڵ� P �� �� P ������Բ��һ������ߵľ������d .��֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ռ�������A(-2,0,2),B(-1,1,2),C(-3,0,4),��![]() =
=![]() ,
,![]() =
=![]() .
.
(1)��![]() ��
��![]() �ļнǵ�����ֵ; (2)��
�ļнǵ�����ֵ; (2)��![]() ��k
��k![]() -2
-2![]() ���ഹֱ,��ʵ��k��ֵ.
���ഹֱ,��ʵ��k��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com