
【题目】甲、乙两位同学从A、B、C、D…共n(n≥2,n∈N+)所高校中,任选两所参加自主招生考试(并且只能选两所高校),但同学甲特别喜欢A高校,他除选A高校外,再在余下的n﹣1所中随机选1所;同学乙对n所高校没有偏爱,在n所高校中随机选2所.若甲同学未选中D高校且乙选中D高校的概率为 ![]() .
.
(1)求自主招生的高校数n;
(2)记X为甲、乙两名同学中未参加D高校自主招生考试的人数,求X的分布列和数学期望.
【答案】
(1)解:由已知得甲同学选中D高校的概率为 ![]() ,
,
乙同学选中D高校的概率p2= ![]() =
= ![]() ,
,
∴甲同学未选中D高校且乙同学选取中D高校的概率为:
p=(1﹣p1)p2=(1﹣ ![]() )×
)× ![]() =
= ![]() ,
,
整理,得 ![]() ﹣23n+40=0,
﹣23n+40=0,
∵n≥2,n∈N*,解得n=5,故自主招生的高校数为5所
(2)解:X的所有可能取值为0,1,2,
P(X=0)= ![]() =
= ![]() ,
,
P(X=1)= ![]() ,
,
P(X=2)= ![]() ,
,
∴X的分布列为:
X | 0 | 2 | 3 |
P |
|
|
|
EX= ![]() =
= ![]() .
.
【解析】(1)由已知得甲同学选中D高校的概率为 ![]() ,乙同学选中D高校的概率p2=
,乙同学选中D高校的概率p2= ![]() =
= ![]() ,甲同学未选中D高校且乙同学选取中D高校的概率为p=(1﹣p1)p2=(1﹣
,甲同学未选中D高校且乙同学选取中D高校的概率为p=(1﹣p1)p2=(1﹣ ![]() )×
)× ![]() =
= ![]() ,由此能求出自主招生的高校数n.(2)X的所有可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和数学期望.
,由此能求出自主招生的高校数n.(2)X的所有可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和数学期望.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】某产品生产厂家根据以往销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),其总成本为g(x)(万元),其中固定成本为2万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本);销售收入R(x)(万元)满足: ![]() 假设该产品产销平衡,试根据上述资料分析:
假设该产品产销平衡,试根据上述资料分析:
(1)要使工厂有盈利,产量x应控制在什么范围内;
(2)工厂生产多少台产品时,可使盈利最多?
(3)当盈利最多时,求每台产品的售价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x和所支出的维修费用y(万元),有如下的统计数据(xi , yi)(i=1,2,3,4,5)由资料知y对x呈线性相关,并且统计的五组数据得平均值分别为 ![]() ,
, ![]() ,若用五组数据得到的线性回归方程
,若用五组数据得到的线性回归方程 ![]() =bx+a去估计,使用8年的维修费用比使用7年的维修费用多1.1万元,
=bx+a去估计,使用8年的维修费用比使用7年的维修费用多1.1万元,
(1)求回归直线方程;
(2)估计使用年限为10年时,维修费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A. 3600 B. 1080 C. 1440 D. 2520
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l经过直线2x+y+5=0与x﹣2y=0的交点,圆C1:x2+y2﹣2x﹣2y﹣4=0与圆C2:x2+y2+6x+2y﹣6=0相较于A、B两点.
(1)若点P(5,0)到直线l的距离为4,求l的直线方程;
(2)若直线l与直线AB垂直,求直线l方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标系与参数方程
在直角坐标系xOy中,曲线M的参数方程为![]() (α为参数),若以直角坐标系中的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线N的极坐标方程为
(α为参数),若以直角坐标系中的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线N的极坐标方程为![]() (t为参数).
(t为参数).
(1)求曲线M的普通方程和曲线N的直角坐标方程;
(2)若曲线N与曲线M有公共点,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.a>b是ac2>bc2的充要条件
B.a>1,b>1是ab>1的充分条件
C.?x0∈R,e ![]() ≤0
≤0
D.若p∨q为真命题,则p∧q为真
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点. (Ⅰ)求证:直线AF∥平面PEC;
(Ⅱ)求PC与平面PAB所成角的正弦值.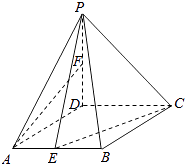
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com