
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在区间
在区间![]() 上的最值;
上的最值;
(2)讨论函数![]() 的单调性;
的单调性;
(3)当![]() 时,有
时,有![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ,
, ![]() ;(2)当
;(2)当![]() 时,
时, ![]() 在
在![]() 单调递增,当
单调递增,当![]() 时,
时, ![]() 在
在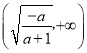 单调递增,在
单调递增,在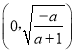 上单调递减,当
上单调递减,当![]() 时,
时, ![]() 在
在![]() 单调递减;(3)
单调递减;(3) ![]() .
.
【解析】试题分析:(1)![]() 在
在![]() 的最值只能在
的最值只能在![]() 和区间的两个端点取到,因此,通过算出上述点并比较其函数值可得函数
和区间的两个端点取到,因此,通过算出上述点并比较其函数值可得函数![]() 在
在![]() 的最值;(2)算出
的最值;(2)算出![]() ,对
,对![]() 的取值范围分情况讨论即可;(3)根据(2)中得到的单调性化简不等式,从而求解不等式,解得
的取值范围分情况讨论即可;(3)根据(2)中得到的单调性化简不等式,从而求解不等式,解得![]() 的取值范围.
的取值范围.
试题解析:(1)当![]() 时,
时, ![]() ,∴
,∴![]() ,
,
∵![]() 的定义域为
的定义域为![]() ,∴由
,∴由![]() ,得
,得![]() .……………………2分
.……………………2分
∴![]() 在区间
在区间![]() 上的最值只可能在
上的最值只可能在![]() 取到,
取到,
而![]() ,
, ![]() ,
, ![]() ,……4分
,……4分
(2)![]() ,
, ![]() ,
,
①当![]() ,即
,即![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 上单调递减;……5分
上单调递减;……5分
②当![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 上单调递增;…………………………6分
上单调递增;…………………………6分
③当![]() 时,由
时,由![]() 得
得![]() ,∴
,∴![]() 或
或![]() (舍去)
(舍去)
∴![]() 在
在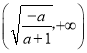 上单调递增,在
上单调递增,在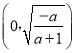 上单调递减;……………………8分
上单调递减;……………………8分
综上,当![]() 时,
时, ![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() 在
在 单调递增,在
单调递增,在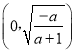 上单调递减.
上单调递减.
当![]() 时,
时, ![]() 在
在![]() 单调递减;
单调递减;
(3)由(2)知,当![]() 时,
时, 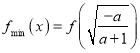 ,
,
即原不等式等价于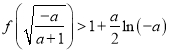 ,…………………………12分
,…………………………12分
即![]() ,整理得
,整理得![]() ,
,
∴![]() ,………………13分
,………………13分
又∵![]() ,∴
,∴![]() 的取值范围为
的取值范围为![]() .……………………14分
.……………………14分


科目:高中数学 来源: 题型:
【题目】某公司为招聘新员工设计了一个面试方案:应聘者从6道备选题中一次性随机抽取3道题,按题目要求独立完成.规定:至少正确完成其中2道题的便可通过.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是![]() ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列及数学期望;
(2)请分析比较甲、乙两人谁面试通过的可能性大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() .
.
(1)若不经过坐标原点的直线![]() 与圆
与圆![]() 相切,且直线
相切,且直线![]() 在两坐标轴上的截距相等,求直线
在两坐标轴上的截距相等,求直线![]() 的方程;
的方程;
(2)设点![]() 在圆
在圆![]() 上,求点
上,求点![]() 到直线
到直线![]() 距离的最大值与最小值.
距离的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “![]() 为真”是“
为真”是“![]() 为真”的充分不必要条件;
为真”的充分不必要条件;
B. 样本![]() 的标准差是3.3;
的标准差是3.3;
C. K2是用来判断两个分类变量是否相关的随机变量,当K2的值很小时可以推定两类变量不相关;
D. 设有一个回归直线方程为![]() ,则变量
,则变量![]() 每增加一个单位,
每增加一个单位,![]() 平均减少1.5个单位.
平均减少1.5个单位.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】性格色彩学创始人乐嘉是江苏电视台当红节目“非诚勿扰”的特约嘉宾,他的点评视角独特,语言犀利,给观众留下了深刻的印象,某报社为了了解观众对乐嘉的喜爱程度,随机调查了观看了该节目的140名观众,得到如下的列联表:(单位:名)
男 | 女 | 总计 | ||||||
喜爱 | 40 | 60 | 100 | |||||
不喜爱 | 20 | 20 | 40 | |||||
总计 | 60 | 80 | 140 | |||||
p(k2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | |||
k0 | 2.705 | 3.841 | 5.024 | 6.635 | 7.879 | |||
(Ⅰ)从这60名男观众中按对乐嘉是否喜爱采取分层抽样,抽取一个容量为6的样本,问样本中喜爱与不喜爱的观众各有多少名?
(Ⅱ)根据以上列联表,问能否在犯错误的概率不超过0.025的前提下认为观众性别与喜爱乐嘉有关?(精确到0.001)
(Ⅲ)从(Ⅰ)中的6名男性观众中随机选取两名作跟踪调查,求选到的两名观众都喜爱乐嘉的概率.
附: 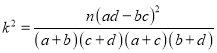
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016高考四川文科】已知数列{![]() }的首项为1,
}的首项为1,![]() 为数列
为数列![]() 的前n项和,
的前n项和,![]() ,其中q>0,
,其中q>0,![]() .
.
(Ⅰ)若![]() 成等差数列,求
成等差数列,求![]() 的通项公式;
的通项公式;
(Ⅱ)设双曲线![]() 的离心率为
的离心率为![]() ,且
,且![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com