
【题目】已知函数![]() ,
, ![]() ,
, ![]() ,且
,且![]() 的最小值为
的最小值为![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,其中
恒成立,其中![]() 是自然对数的底数,求
是自然对数的底数,求![]() 的取值范围;
的取值范围;
(3)设曲线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,且两曲线在点
,且两曲线在点![]() 处的切线分别为
处的切线分别为![]() ,
, ![]() .试判断
.试判断![]() ,
, ![]() 与
与![]() 轴是否能围成等腰三角形?若能,确定所围成的等腰三角形的个数;若不能,请说明理由.
轴是否能围成等腰三角形?若能,确定所围成的等腰三角形的个数;若不能,请说明理由.
【答案】(1)![]() .(2)
.(2)![]() . (3)
. (3)![]() ,
, ![]() 与
与![]() 轴能围成2个等腰三角形.
轴能围成2个等腰三角形.
【解析】试题分析:
(1)由原函数与导函数的关系可求得a=-2;
(2) 不等式即![]() ,构造函数令
,构造函数令![]() ,分类讨论可得
,分类讨论可得![]() 的取值范围是
的取值范围是![]() .
.
(3) 设![]() ,
, ![]() 的倾斜角分别为
的倾斜角分别为![]() ,
, ![]() ,若
,若![]() ,
, ![]() 与
与![]() 轴所围成的三角形是等腰三角形,则
轴所围成的三角形是等腰三角形,则![]() 或
或![]() . 分类讨论:
. 分类讨论: ![]() 和
和![]() 两种情况可得
两种情况可得![]() ,
, ![]() 与
与![]() 轴能围成2个等腰三角形.
轴能围成2个等腰三角形.
试题解析:
(1)![]() ,所以
,所以![]() ,则
,则![]() 的最小值为
的最小值为![]() ,
,
因此抛物线![]() 的对称轴为
的对称轴为![]() ,即
,即![]() ,所以
,所以![]() .
.
(2)由(1)知, ![]() .不等式
.不等式![]() 即
即![]() ,
,
所以![]() 对任意
对任意![]() 恒成立.
恒成立.
令![]() ,则
,则![]() .
.
①若![]() ,则
,则![]() ,所以函数
,所以函数![]() 在
在![]() 上单调减,
上单调减,
故![]() ,解得
,解得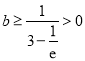 ,
,
此时无符合题意的![]() 值; ②若
值; ②若![]() ,令
,令![]() ,解得
,解得![]() .
.
列表如下:
|
|
|
|
|
|
|
|
| ↘ | 极小值 | ↗ |
由题意,可知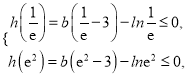 解得
解得![]() .
.
故![]() 的取值范围为
的取值范围为![]() .
.
(3)设![]() ,
, ![]() 的倾斜角分别为
的倾斜角分别为![]() ,
, ![]() ,则
,则![]() ,
, ![]() .
.
因为![]() ,所以
,所以![]() ,
, ![]() ,则
,则![]() ,
, ![]() 均为锐角.
均为锐角.
若![]() ,
, ![]() 与
与![]() 轴所围成的三角形是等腰三角形,则
轴所围成的三角形是等腰三角形,则![]() 或
或![]() .
.
①当![]() 时,
时, ![]() ,即
,即![]() ,解得
,解得![]() ,
,
而![]() ,即
,即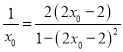 ,
,
整理得, ![]() ,解得
,解得![]() .
.
所以存在唯一的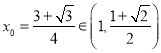 满足题意.
满足题意.
②当![]() 时,由
时,由![]() 可得
可得![]() ,
,
而![]() ,即
,即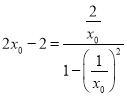 ,
,
整理得, ![]() .
.
令![]() ,则
,则![]() .
.
令![]() ,解得
,解得![]() .列表如下:
.列表如下:
|
|
|
|
|
|
|
|
| ↘ | 极小值 | ↗ |
而![]() ,
, ![]() ,
, ![]() ,
,
所以![]() 在
在![]() 内有一个零点,也是
内有一个零点,也是![]() 上的唯一零点.
上的唯一零点.
所以存在唯一的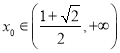 满足题意.
满足题意.
综上所述, ![]() ,
, ![]() 与
与![]() 轴能围成2个等腰三角形.
轴能围成2个等腰三角形.


科目:高中数学 来源: 题型:
【题目】已知抛物线x2=2py(p>0)与直线2x﹣y+1=0交于A,B两点, ![]() ,点M在抛物线上,MA⊥MB.
,点M在抛物线上,MA⊥MB. 
(1)求p的值;
(2)求点M的横坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+bx+c,且f(﹣3)=f(1),f(0)=0.
(1)求函数f(x)的解析式;
(2)若函数g(x)=f(x)﹣(4+2a)x+2,x∈[1,2],求函数g(x)的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《张邱建算经》是中国古代数学史上的杰作,该书中有首古民谣记载了一数列问题:“南山一棵竹, 竹尾风割断, 剩下三十节,一节一个圈. 头节高五寸①,头圈一尺三②.逐节多三分③,逐圈少分三④. 一蚁往上爬,遇圈则绕圈. 爬到竹子顶,行程是多远?”(注释:①第一节的高度为![]() 尺;②第一圈的周长为
尺;②第一圈的周长为![]() 尺;③每节比其下面的一节多
尺;③每节比其下面的一节多![]() 尺;④每圈周长比其下面的一圈少
尺;④每圈周长比其下面的一圈少![]() 尺) 问:此民谣提出的问题的答案是
尺) 问:此民谣提出的问题的答案是
A. ![]() 尺 B.
尺 B. ![]() 尺
尺
C. ![]() 尺 D.
尺 D. ![]() 尺
尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() ,不经过原点O的直线l:y=kx+m(k>0)与椭圆E相交于不同的两点A、B,直线OA,AB,OB的斜率依次构成等比数列.
,不经过原点O的直线l:y=kx+m(k>0)与椭圆E相交于不同的两点A、B,直线OA,AB,OB的斜率依次构成等比数列. 
(Ⅰ)求a,b,k的关系式;
(Ⅱ)若离心率 ![]() 且
且 ![]() ,当m为何值时,椭圆的焦距取得最小值?
,当m为何值时,椭圆的焦距取得最小值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣4x+3,若f(x)≥mx对任意的实数x≥2都成立,则实数m的取值范围是( )
A.[﹣2 ![]() ﹣4,﹣2
﹣4,﹣2 ![]() ?+4]
?+4]
B.(﹣∞,﹣2 ![]() ﹣4]∪[﹣2
﹣4]∪[﹣2 ![]() ?+4,+∞)
?+4,+∞)
C.[﹣2 ![]() ?+4,+∞)
?+4,+∞)
D.(﹣∞,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x2﹣2ax)(a>0且a≠1)满足对任意的x1 , x2∈[3,4],且x1≠x2时,都有 ![]() >0成立,则实数a的取值范围是
>0成立,则实数a的取值范围是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com