
【题目】如图是求样本x1、x2、…x10平均数 ![]() 的程序框图,图中空白框中应填入的内容为( )
的程序框图,图中空白框中应填入的内容为( ) 
A.S=S+xn
B.S=S+ ![]()
C.S=S+n
D.S=S+ ![]()
【答案】A
【解析】解:由题目要求可知:该程序的作用是求样本x1 , x2 , …,x10平均数 ![]() , 由于“输出
, 由于“输出 ![]() ”的前一步是“
”的前一步是“ ![]() =
= ![]() ”,
”,
故循环体的功能是累加各样本的值,
故应为:S=S+xn
故选:A.
【考点精析】根据题目的已知条件,利用平均数、中位数、众数和程序框图的相关知识可以得到问题的答案,需要掌握⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据;程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() ,g(x)=
,g(x)= ![]() ﹣1. (Ⅰ)若a>0,试判断f(x)在定义域内的单调性;
﹣1. (Ⅰ)若a>0,试判断f(x)在定义域内的单调性;
(Ⅱ)若f(x)在[1,e]上的最小值为 ![]() ,求a的值;
,求a的值;
(Ⅲ)当a=0时,若x≥1时,恒有xf(x)≤λ[g(x)+x]成立,求λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,∠ACB=90°,BB1=3,AC=BC=2,D,E分别为AB,BC的中点,F为BB1上一点,且 ![]() =
= ![]() .
. 
(1)求证:平面CDF⊥平面A1C1E;
(2)求二面角C1﹣CD﹣F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( ) 
A.与平面A1DE垂直的直线必与直线BM垂直
B.异面直线BM与A1E所成角是定值
C.一定存在某个位置,使DE⊥MO
D.三棱锥A1﹣ADE外接球半径与棱AD的长之比为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A是抛物线y2=4x上的一点,以点A和点B(2,0)为直径的圆C交直线x=1于M,N两点.直线l与AB平行,且直线l交抛物线于P,Q两点. (Ⅰ)求线段MN的长;
(Ⅱ)若 ![]() =﹣3,且直线PQ与圆C相交所得弦长与|MN|相等,求直线l的方程.
=﹣3,且直线PQ与圆C相交所得弦长与|MN|相等,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取100名市民,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如下:
分组(岁) | 频数 |
[25,30) | x |
[30,35) | y |
[35,40) | 35 |
[40,45) | 30 |
[45,50] | 10 |
合计 | 100 |
(Ⅰ)求频率分布表中x、y的值,并补全频率分布直方图;
(Ⅱ)在抽取的这100名市民中,按年龄进行分层抽样,抽取20人参加国产手机用户体验问卷调查,现从这20人重随机抽取2人各赠送精美礼品一份,设这2名市民中年龄在[35,40)内的人数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《孙子算经》是我国古代的数学著作,其卷下中有类似如下的问题:“今有方物一束,外周一匝有四十枚,问积几何?”如右图是解决该问 题的程序框图,若设每层外周枚数为a,则输出的结果为( )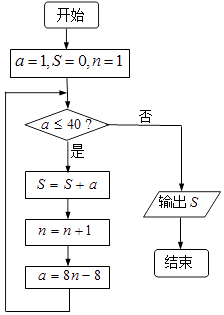
A.81
B.74
C.121
D.169
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() 的左右焦点分别为F1 , F2 , 过右焦点F2的直线交双曲线于A,B两点,连接AF1 , BF1 . 若|AB|=|BF1|,且∠ABF1=90°,则双曲线的离心率为 .
的左右焦点分别为F1 , F2 , 过右焦点F2的直线交双曲线于A,B两点,连接AF1 , BF1 . 若|AB|=|BF1|,且∠ABF1=90°,则双曲线的离心率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A、B、C的对边分别为a、b、c,已知△ABC的面积为accosB,BC的中点为D. (Ⅰ) 求cosB的值;
(Ⅱ) 若c=2,asinA=5csinC,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com