

 ,其中
,其中 ,若点
,若点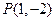 在矩阵
在矩阵 的变换下得到点
的变换下得到点 ,
, 的特征值及其对应的特征向量.
的特征值及其对应的特征向量. ,圆
,圆 的参数方程为
的参数方程为
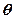 为参数).
为参数). 上的点到直线的距离的最小值.
上的点到直线的距离的最小值.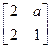
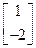 =
=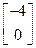 ,∴
,∴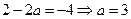 . -------------------3分
. -------------------3分
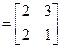 ,则矩阵
,则矩阵 的特征多项式为
的特征多项式为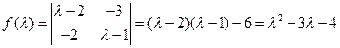 --------------------------5分
--------------------------5分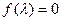 ,得矩阵
,得矩阵 的特征值为
的特征值为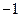 与4. (5分)
与4. (5分)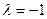 时,
时,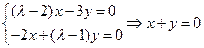
 的属于特征值
的属于特征值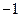 的一个特征向量为
的一个特征向量为 ; ---------------------------------6分
; ---------------------------------6分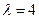 时,
时,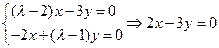
 的属于特征值
的属于特征值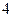 的一个特征向量为
的一个特征向量为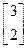 . ------------------------------7分
. ------------------------------7分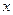 轴正半轴建立直角坐标系. ----------------1分
轴正半轴建立直角坐标系. ----------------1分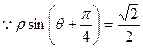
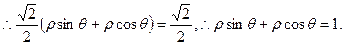 ----------------2分
----------------2分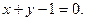 ----------------3分
----------------3分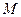 的普通方程为:
的普通方程为: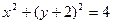 ----------------4分
----------------4分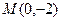 到直线
到直线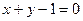 的距离
的距离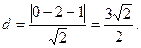 ---------------5分
---------------5分 上的点到直线的距离的最小值为
上的点到直线的距离的最小值为 ----------------7分
----------------7分

科目:高中数学 来源:不详 题型:解答题
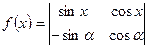 ,
,
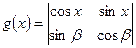 ,
, 是参数,
是参数,  ,
,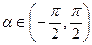 ,
,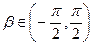
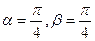 ,判别
,判别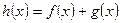 的奇偶性;
的奇偶性; 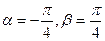 ,判别
,判别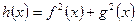 的奇偶性; (6分)
的奇偶性; (6分)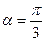 ,
,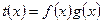 是偶函数,求
是偶函数,求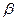 (4分)
(4分)
 推广或是问题(2)的推广,问题(1)或(2)是问题(3)的特例。(不必证明命题)
推广或是问题(2)的推广,问题(1)或(2)是问题(3)的特例。(不必证明命题)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
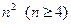 个正数排成
个正数排成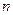 行
行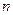 列方阵:符号
列方阵:符号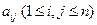 表示位于第
表示位于第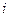 行第
行第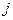 列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且每一
列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且每一 列的数的公比都等于
列的数的公比都等于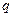 . 若
. 若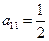 ,
,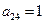 ,
,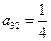 , 则
, 则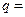 ________,
________,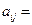 __________.
__________.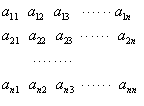
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com