

| 外语 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 8 | m | 9 |
| 良 | 9 | n | 11 | |
| 及格 | 8 | 9 | 11 | |
分析 (Ⅰ)根据简单随机抽样的定义即可得到结论,
(Ⅱ)根据数学成绩优秀率是35%,构造关于m的方程,解方程可得m值,进而根据抽取样本容量为100,可得n值;
(Ⅲ)由题意m+n=35,且m≥12,n≥10,所以满足条件的(m,n)的基本事件总数及满足数学成绩优比良的人数少的基本事件个数,代入古典概型概率计算公式,可得答案.
解答 解:(Ⅰ)根据图表数据第一个数为544,依次为354,378,520,384,
(Ⅱ)由$\frac{8+m+9}{100}$=0.35,得m=18
因为8+9+8+18+n+9+9+11+11=100,
所以n=17,
(Ⅲ)由题意m+n=35,且m≥12,n≥10,
所以满足条件的(m,n)有:
(12,23),(13,22),(14,21),(15,20),(16,19),(17,18),(18,17),
(19,16),(20,15),(21,14),(22,13),(23,12),(24,11),(25,10),
共有14种,且每组出现都是等可能的,
记:“数学成绩优秀的人数比良的人数少”为事件M,
事件M包括:(12,23),(13,22),(14,21),(15,20),(16,19),(17,18)共6个基本事件,
∴P(M)=$\frac{6}{14}$=$\frac{3}{7}$.
点评 本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | (-$\frac{3}{4}$-ln2,1] | C. | (-$\frac{3}{4}$-ln2,+∞) | D. | (-∞,-$\frac{3}{4}$-ln2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,四棱锥S-ABCD的底面四边形ABCD为平行四边形,其中AC⊥BD,且AC、BD相交于O,∠SBC=∠SBA.
如图所示,四棱锥S-ABCD的底面四边形ABCD为平行四边形,其中AC⊥BD,且AC、BD相交于O,∠SBC=∠SBA.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11,25 | B. | 11,27 | C. | 8,27 | D. | 11,8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
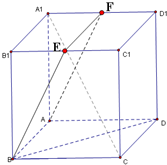 在单位正方体ABCD-A1B1C1D1中,E,F分别是B1C1,A1D1的中点.
在单位正方体ABCD-A1B1C1D1中,E,F分别是B1C1,A1D1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com