
分析 (1)n=1时,袋中的白球的个数可能为a个(即取出的是白球),也可能为a+1个(即取出的是黑球),由此能求出EX1.
(2)$P({X_{n+1}}=a+0)={P_0}•\frac{a}{a+b}$,k≥1时,第n+1次取出来有a+k个白球的可能性有两种;第n次袋中有a+k个白球,a+b个白球,第n+1次取出来的也是白球;第n次袋中有a+k-1个白球,第n+1次取出来的是黑球,由于每次球的总数为a+b个,此时黑球的个数为b-k+1.由此能求出P(Xn+1=a+k),k=0,1,…,b.
(3)第n+1次白球的个数的数学期望分为两类:第n次白球个数的数学期望,即EXn.由于白球和黑球的总个数为a+b,第n+1次取出来的是白球;第n+1次取出来的是黑球.由此能证明:$E{X_{n+1}}=(1-\frac{1}{a+b})E{X_n}+1$.
解答 解:(1)n=1时,袋中的白球的个数可能为a个(即取出的是白球),概率为$\frac{a}{a+b}$;
也可能为a+1个(即取出的是黑球),概率为$\frac{b}{a+b}$,
故$E{X_1}=a•\frac{a}{a+b}+(a+1)•\frac{b}{a+b}=\frac{{{a^2}+ab+b}}{a+b}$.
(2)首先,$P({X_{n+1}}=a+0)={P_0}•\frac{a}{a+b}$;
k≥1时,第n+1次取出来有a+k个白球的可能性有两种;
第n次袋中有a+k个白球,显然每次取出球后,球的总数保持不变,
即a+b个白球(故此时黑球有b-k个),第n+1次取出来的也是白球,
这种情况发生的概率为${P_k}•\frac{a+k}{a+b}$;
第n次袋中有a+k-1个白球,第n+1次取出来的是黑球,由于每次球的总数为a+b个,
故此时黑球的个数为b-k+1.
这种情况发生的概率为${P_{k-1}}•\frac{b-k+1}{a+b}(k≥1)$.
故$P({X_{n+1}}=a+k)={P_k}•\frac{a+k}{a+b}+{P_{k-1}}•\frac{b-k+1}{a+b}(k≥1)$.
(3)第n+1次白球的个数的数学期望分为两类:
第n次白球个数的数学期望,即EXn.由于白球和黑球的总个数为a+b,第n+1次取出来的是白球,
这种情况发生的概率是$\frac{{E{X_n}}}{a+b}$;
第n+1次取出来的是黑球,这种情况发生的概率是$\frac{{a+b-E{X_n}}}{a+b}$,
此时白球的个数是EXn+1.
故$E{X_{n+1}}=\frac{{E{X_n}}}{a+b}E{X_n}+\frac{{a+b-E{X_n}}}{a+b}•(E{X_n}+1)=\frac{{{{(E{X_n})}^2}}}{a+b}+(1-\frac{{E{X_n}}}{a+b})(E{X_n}+1)$
=EXn+1-$\frac{E{X}_{n}}{a+b}$.
∴:$E{X_{n+1}}=(1-\frac{1}{a+b})E{X_n}+1$.
点评 本题考查离散型随机变量的分布列及数学期望的求法及证明,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x}$ | B. | y=-x+$\frac{1}{x}$ | ||
| C. | y=-x|x| | D. | y=$\left\{\begin{array}{l}{-x+1,x>0}\\{-x-1,x≤0}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{24}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{8}$ | D. | $\frac{11π}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 3 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
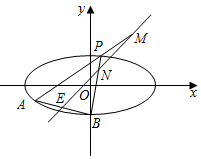 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),点B是其下顶点,直线x+3y+6=0与椭圆C交于A,B两点(点A在x轴下方),且线段AB的中点E在直线y=x上.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),点B是其下顶点,直线x+3y+6=0与椭圆C交于A,B两点(点A在x轴下方),且线段AB的中点E在直线y=x上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com