
(附加题,10分)已知函数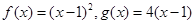 ,数列
,数列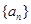 满足
满足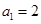 ,且
,且 .
.
(1)试探究数列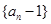 是否是等比数列?(5分)
是否是等比数列?(5分)
(2)试证明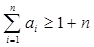 .(5分)
.(5分)
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
等比数列 满足
满足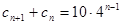 ,
, ,数列
,数列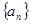 满足
满足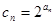
(1)求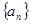 的通项公式;(5分)
的通项公式;(5分)
(2)数列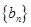 满足
满足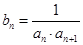 ,
,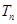 为数列
为数列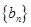 的前
的前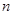 项和.求
项和.求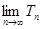 ;(5分)
;(5分)
(3)是否存在正整数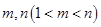 ,使得
,使得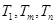 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有 的值;若不存在,请说明理由.(6分)
的值;若不存在,请说明理由.(6分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知数列{an}的前n项和为Sn,点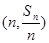 在直线
在直线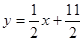 上.数列{bn}满足
上.数列{bn}满足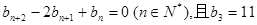 ,前9项和为153.
,前9项和为153.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)设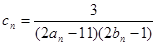 ,数列{cn}的前n和为Tn,求使不等式
,数列{cn}的前n和为Tn,求使不等式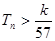 对一切
对一切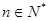 都成立的最大正整数k的值.
都成立的最大正整数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列 和
和 满足:
满足: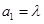 ,
,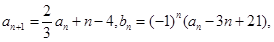 其中
其中 为实数,
为实数,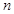 为正整数.
为正整数.
(Ⅰ)对任意实数 ,证明数列
,证明数列 不是等比数列;
不是等比数列;
(Ⅱ)对于给定的实数 ,试求数列
,试求数列 的前
的前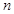 项和
项和 ;
;
(Ⅲ)设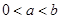 ,是否存在实数
,是否存在实数 ,使得对任意正整数
,使得对任意正整数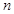 ,都有
,都有 成立? 若存在,求
成立? 若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com