
分析 (Ⅰ)由$\left\{\begin{array}{l}x+1>0\\ 1-x>0\end{array}\right.$ 可得函数f(x)+g(x)的定义域;
(Ⅱ)根据F(-x)=F(x),可得:函数F (x)是偶函数
(Ⅲ)F(x)=f(x)+g(x)在区间(0,1)上是减函数,作差可证明结论.
解答 (Ⅰ)解:要函数有意义,则$\left\{\begin{array}{l}x+1>0\\ 1-x>0\end{array}\right.$ (2分)
∴-1<x<1,
即函数的定义域为(-1,1)(4分)
(Ⅱ)解:令F(x)=f(x)+g(x)=lg(x+1)+lg(1-x)=lg(1-x2).
由(1)得函数定义域关于原点对称
又F(-x)=F(x),
∴函数F (x)是偶函数.(6分)
(Ⅲ)解:F(x)=f(x)+g(x)在区间(0,1)上是减函数,
理由如下:
设x1、x2∈(0,1),x1<x2,
则$1-{{x}_{1}}^{2}>1-{{x}_{2}}^{2}>0$,即$\frac{1-{{x}_{1}}^{2}}{1-{{x}_{2}}^{2}}$>1,
∴F (x1)-F(x2)=lg(1-x12)-lg(1-x22)=lg$\frac{1-{{x}_{1}}^{2}}{1-{{x}_{2}}^{2}}$>0.
即F (x1)>F(x2)
∴F(x)=f(x)+g(x)在区间(0,1)上是减函数.(12分)
点评 本题考查的知识点是函数的定义域,函数的奇偶性,函数的单调性,难度中档.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:选择题
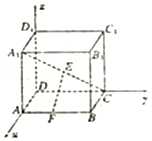 如图所示,在空间直角坐标系中,D是坐标原点,有一棱长为a的正方体ABCD-A1B1C1D1,E和F分别是体对角线A1C和棱AB上的动点,则|EF|的最小值为( )
如图所示,在空间直角坐标系中,D是坐标原点,有一棱长为a的正方体ABCD-A1B1C1D1,E和F分别是体对角线A1C和棱AB上的动点,则|EF|的最小值为( )| A. | $\sqrt{2}a$ | B. | $\frac{{\sqrt{2}}}{2}a$ | C. | a | D. | $\frac{1}{2}a$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
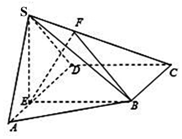 如图,在四棱锥S-ABCD中,平面SAD⊥底面ABCD,$∠SAD=\frac{π}{3}$,在AD边上取一点E,使得BCDE为矩形,SA=2AE=DE=2.
如图,在四棱锥S-ABCD中,平面SAD⊥底面ABCD,$∠SAD=\frac{π}{3}$,在AD边上取一点E,使得BCDE为矩形,SA=2AE=DE=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
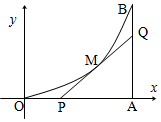 如图,由y=0,x=8,y=x2围成的曲边三角形,在曲线OB弧上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围城的三角形PQA的面积最大,并求得最大值.
如图,由y=0,x=8,y=x2围成的曲边三角形,在曲线OB弧上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围城的三角形PQA的面积最大,并求得最大值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\sqrt{3}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y+6=0 | B. | x-2y-6=0 | C. | x+2y-10=0 | D. | x+2y-8=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com