
| A. | 200 | B. | 180 | C. | 150 | D. | 280 |
分析 根据题意,分2步进行分析,①、先将5个人分成3组,分析可得有2种分组方法:分成2-2-1的三组或分成3-1-1的三组,分别求出每种情况的分组方法数目,由分类计数原理可得分组方法数目,②、将分好的3组对应三个班级,由排列数公式可得其方法数目,进而由分步计数原理计算可得答案.
解答 解:根据题意,分2步进行分析,
①、先将5个人分成3组,
若分成2-2-1的三组,有$\frac{{C}_{5}^{2}{C}_{3}^{2}{C}_{1}^{1}}{{A}_{2}^{2}}$=15种情况,
若分成3-1-1的三组,有$\frac{{C}_{5}^{3}{C}_{2}^{1}{C}_{1}^{1}}{{A}_{2}^{2}}$=10种情况,
一共有15+10=25种分组方法;
②、将分好的3组对应三个班级,有${A}_{3}^{3}$=6种方法,
则一共有25×6=150种不同分派方法,
故选:C.
点评 本题考查排列、组合的应用,要先将5名学生分成3组,再将其分配到三个班级.


科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {1,2} | C. | {1,2,3} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
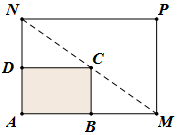 如图所示,某小区内有一矩形花坛,现将这一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知AB=3米,AD=2米.
如图所示,某小区内有一矩形花坛,现将这一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知AB=3米,AD=2米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
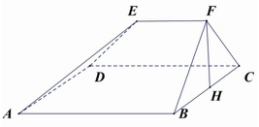 如图,多面体ABCDEF中,已知ABCD是边长为3的正方形,△FBC中BC边上的高为FH,EF⊥FH,EF∥AB,
如图,多面体ABCDEF中,已知ABCD是边长为3的正方形,△FBC中BC边上的高为FH,EF⊥FH,EF∥AB,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
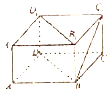
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{15}}}{5}$ | D. | $\frac{{\sqrt{10}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}+\frac{3}{2}i$ | B. | $\frac{1}{2}-\frac{3}{2}i$ | C. | $\frac{1}{2}+\frac{3}{2}i$ | D. | $\frac{3}{2}-\frac{3}{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
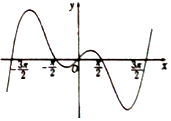
| A. | f(x)=x+sinx | B. | f(x)=$\frac{cosx}{x}$ | C. | f(x)=x(x-$\frac{π}{2}$)(x-$\frac{3π}{2}$) | D. | f(x)=xcosx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com