
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 可以设圆上一点P(x0,y0),由∠APB=90°,可得AP⊥BP,kAP•kBP=-1,然后的到关于t的关系式,求解t的最小值.
解答 解:设P点坐标(x0,y0),kAP•kBP=$\frac{{y}_{0}}{{x}_{0}+t}•\frac{{y}_{0}}{{x}_{0}-t}=-1$,
整理得${{x}_{0}}^{2}+{{y}_{0}}^{2}={t}^{2}$,即$t=\sqrt{{{x}_{0}}^{2}+{{y}_{0}}^{2}}$=${\sqrt{({x}_{0}-0)^{2}+({y}_{0}-0)}}^{2}$
由此可以将求t的最小值问题看做点P到原点的最短距离问题,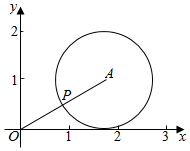
如图所示,当P点在如图位置时,OP的距离最小,即t取得最小值,
A点坐标($\sqrt{3}$,1)易知OA所在直线方程为:y=$\frac{\sqrt{3}}{3}x$,联立圆的方程:(x-$\sqrt{3}$)2+(y-1)2=1,可得P点坐标($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)
从而|OP|=$\sqrt{(\frac{\sqrt{3}}{2})^{2}+(\frac{1}{2})^{2}}$=1,即t=1.故t的最小值为1.
故选:D.
点评 本题考察圆与直线方程的综合应用以及两点间距离公式,解决此类问题,注意采用数形结合思想,可较快得到答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱的长度是( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱的长度是( )| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 6 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
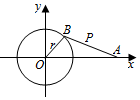 如图,OB是机器的曲柄,长是r,绕点O转动,AB是连杆,长为l,点A在直线Ox上往返运动,点P是AB的中点,当点B绕点O作圆周运动,求点P的轨迹的参数方程.
如图,OB是机器的曲柄,长是r,绕点O转动,AB是连杆,长为l,点A在直线Ox上往返运动,点P是AB的中点,当点B绕点O作圆周运动,求点P的轨迹的参数方程.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | z的虚部为3i | |
| B. | z的共轭复数为1-3i | |
| C. | |z|=4 | |
| D. | z在复平面内对应的点在第三象限内 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com