Question

6．已知双曲线x²-y²=1的左、右顶点分别为A₁、A₂，动直线l：y=kx+m与圆x²+y²=1相切，且与双曲线左、右两支的交点分别为P₁（x₁，y₁），P₂（x₂，y₂），则x₂-x₁的最小值为（　　）

• A． $2\sqrt{2}$
• B． 2
• C． 4
• D． $3\sqrt{2}$

Answer 1

分析 根据直线和圆相切，建立m，k的关系，联立直线和双曲线，转化为一元二次方程，利用根与系数之间的关系进行求解即可．

解答 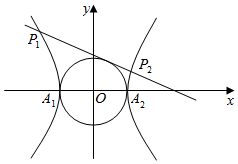解：∵l与圆相切，∴原点到直线的距离d=$\frac{|m|}{\sqrt{1+{k}^{2}}}=1$，
∴m²=1+k²
由$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}-{y}^{2}=1}\end{array}\right.$，得（1-k²）x²-2mkx-（m²+1）=0，
∵直线l：y=kx+m与圆x²+y²=1相切，且与双曲线左、右两支交于两点，
∴$\left\{\begin{array}{l}{1-{k}^{2}≠0}\\{△=4{m}^{2}{k}^{2}+4（1-{k}^{2}）（{m}^{2}+1）=4（{m}^{2}+1-{k}^{2}）=8＞0}\\{{x}_{1}{x}_{2}=\frac{1+{m}^{2}}{{k}^{2}-1}＜0}\end{array}\right.$
∴k²＜1，∴-1＜k＜1，故k的取值范围为（-1，1）．
由于x₁+x₂=$\frac{2mk}{1-{k}^{2}}$，
∴x₂-x₁=$\sqrt{（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}}$=$\frac{2\sqrt{2}}{|1-{k}^{2}|}$=$\frac{2\sqrt{2}}{1-{k}^{2}}$，
∵0≤k²＜1，
∴当k²=0时，x₂-x₁取最小值2$\sqrt{2}$．
故选：A

点评 本题主要考查直线和双曲线位置关系的应用，根据直线和圆的相切的关系，利用转化法，转化为根与系数之间的关系是解决本题的关键．