
���� �������������������ʾ�õ�f��x�������ݺ����ø����ǹ�ʽ�������������ڹ�ʽ��ص�ֵ��
������f��C��=1���C������֪�õ�sinBcosA=3sinAcosA��Ȼ���cosA=0��cosA��0���������á�ABC�������
��� �⣺����$\overrightarrow{a}$=��sin��x+cos��x��$\sqrt{3}$cos��x����$\overrightarrow{b}$=��cos��x-sin��x��2sin��x����
��f��x��=$\overrightarrow{a}$•$\overrightarrow{b}$=${cos^2}��x-{sin^2}��x+2\sqrt{3}cos��x•sin��x$=$cos2��x+\sqrt{3}sin2��x$=$2sin��2��x+\frac{��}{6}��$��
�ߦأ�0���ຯ��f��x��������T=$\frac{2��}{2��}=��$�����=1��
�����ɣ��ã�$f��x��=2sin��2x+\frac{��}{6}��$��
��f��C��=1����$sin��2C+\frac{��}{6}��=\frac{1}{2}$����$\frac{��}{6}��2C+\frac{��}{6}��\frac{13}{6}��$��
��$2C+\frac{��}{6}=\frac{5}{6}��$����$C=\frac{��}{3}$��
�� C=��-��A+B������sinC=sin��B+A��=sinBcosA+cosBsinA��
��sinC+sin��B-A��=3sin2A��
��sinBcosA+cosBsinA+sinBcosA-cosBsinA=6sinAcosA��
������sinBcosA=3sinAcosA��
��cosA=0����A=$\frac{��}{2}$ʱ����ABC��ֱ�������Σ���B=$\frac{��}{6}$��
����b=ctanB=2tan$\frac{��}{6}$=$\frac{2\sqrt{3}}{3}$����S��ABC=$\frac{1}{2}$bc=$\frac{2\sqrt{3}}{3}$��
��cosA��0����sinB=3sinA�������Ҷ�����b=3a����
�����Ҷ����ã�c2=a2+b2-2abcos60���
�����٢ڣ����c=2�����a=$\frac{2\sqrt{7}}{7}$��b=$\frac{6\sqrt{7}}{7}$��
��S��ABC=$\frac{1}{2}$absinC=$\frac{1}{2}$��$\frac{2\sqrt{7}}{7}$��$\frac{6\sqrt{7}}{7}$��$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{7}$��
���ϣ���ABC�����Ϊ$\frac{2\sqrt{3}}{3}$��$\frac{3\sqrt{3}}{7}$��
���� ���⿼�����Ǻ����еĺ�ȱ任Ӧ�ã�������ƽ�����������������㣬ѵ�����������Ҷ��������Ҷ�����������Σ����е��⣮


 ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д� Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������C1��y2=2px����ԲC2��$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1�ڵ�һ���Ľ���ΪB��OΪ����ԭ�㣬AΪ��Բ���Ҷ��㣬��OAB�����Ϊ$\frac{8\sqrt{6}}{3}$��
��ͼ��������C1��y2=2px����ԲC2��$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1�ڵ�һ���Ľ���ΪB��OΪ����ԭ�㣬AΪ��Բ���Ҷ��㣬��OAB�����Ϊ$\frac{8\sqrt{6}}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $2\sqrt{2}$ | B�� | 2 | C�� | 4 | D�� | $3\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
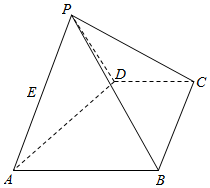 ����ABCD�У�AB��CD��BC��AB����BC=CD=$\frac{1}{2}$AB=1����PADΪ����ֱ�������Σ���APD=90�㣬��ƽ��PAD��ƽ��ABCD��
����ABCD�У�AB��CD��BC��AB����BC=CD=$\frac{1}{2}$AB=1����PADΪ����ֱ�������Σ���APD=90�㣬��ƽ��PAD��ƽ��ABCD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com