
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
分析 先根据抛物线方程求得焦点坐标,进而设出过焦点弦的直线方程,与抛物线方程联立消去y,根据韦达定理表示出x1+x2=2+$\frac{4}{{k}^{2}}$,x1x2=1,y1y2=-4,由$\overrightarrow{MA}$•$\overrightarrow{MB}$=0,求得k值.
解答 解:∵抛物线的方程为y2=4x,∴F(1,0),设焦点弦方程为y=k(x-1),A(x1,y1),B(x2,y2),
代入抛物线方程得k2x2-(2k2+4)x+k2=0
由韦达定理:x1+x2=2+$\frac{4}{{k}^{2}}$,x1x2=1,y1y2=-4,y1+y2=$\frac{4}{k}$
∵M(-1,2),$\overrightarrow{MA}$•$\overrightarrow{MB}$=0,
∴(x1+1,y1-2)•(x2+1,y2-2)=0,
∴1-2k+k2=0,
∴k=1.
故选:C.
点评 本题主要考查了抛物线的简单性质,考查运算求解能力,考查数形结合思想、化归与转化思想,属于中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
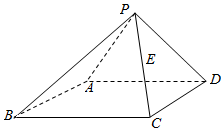 如图所示,在四棱锥P-ABCD中,ABCD为矩形,PA⊥PD,平面PAD⊥平面ABCD,且AB=6,AD=4,PA=PD,E位PC的中点
如图所示,在四棱锥P-ABCD中,ABCD为矩形,PA⊥PD,平面PAD⊥平面ABCD,且AB=6,AD=4,PA=PD,E位PC的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | 2 | C. | 4 | D. | $3\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com