
分析 (Ⅰ)由三角恒等变换化简2cos2A+cos(2A+$\frac{π}{3}$)=-$\frac{1}{2}$,
结合A的取值范围,即可求出A的值;
(Ⅱ)根据△ABC的面积公式求出b的值,再利用余弦定理求出a的值.
解答 解:(Ⅰ)△ABC中,2cos2A+cos(2A+$\frac{π}{3}$)=-$\frac{1}{2}$,
∴2•$\frac{1+cos2A}{2}$+cos(2A+$\frac{π}{3}$)=-$\frac{1}{2}$,
即1+cos2A+cos2Acos$\frac{π}{3}$-sin2Asin$\frac{π}{3}$=-$\frac{1}{2}$,
∴$\frac{\sqrt{3}}{2}$sin2A-$\frac{3}{2}$cos2A=$\frac{3}{2}$,
∴$\frac{1}{2}$sin2A-$\frac{\sqrt{3}}{2}$cos2A=$\frac{\sqrt{3}}{2}$,
即sin(2A-$\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$;
又△ABC是锐角三角形,∴0<A<$\frac{π}{2}$,
∴-$\frac{π}{3}$<2A-$\frac{π}{3}$<$\frac{2π}{3}$,
∴2A-$\frac{π}{3}$=$\frac{π}{3}$,
解得A=$\frac{π}{3}$;
(Ⅱ)c=3,且△ABC的面积为S△ABC=$\frac{1}{2}$bcsinA=$\frac{3b}{2}×\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
解得b=4;
由余弦定理得
a2=b2+c2-2bccosA=42+32-2×4×3×$\frac{1}{2}$=13,
解得a=$\sqrt{13}$.
点评 本题考查了正弦、余弦定理的应用问题,也考查了三角恒等变换问题,是综合性题目.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+i | B. | 1-i | C. | $\frac{{\sqrt{2}}}{2}-\frac{{\sqrt{2}}}{2}i$ | D. | $\frac{{\sqrt{2}}}{2}+\frac{{\sqrt{2}}}{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2a | B. | a | C. | 2 | D. | a或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线x=1对称 | B. | 直线x=-1对称 | C. | 点(1,0)对称 | D. | 点(-1,0)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
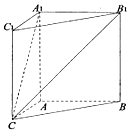 如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com