
分析 (I)利用${log_2}\frac{5}{3}<{2^{0.6}}$,即可得出.
(Ⅱ)$f(x)=\left\{\begin{array}{l}sinx,x∈(kπ+\frac{π}{4},kπ+\frac{3π}{4})(k∈Z)\\ cosx,x∈(kπ+\frac{3π}{4},kπ+\frac{5π}{4})(k∈Z).\end{array}\right.$,可得f(x)的性质:奇偶性,周期性,单调性,最值,进而得出.
解答 解:(Ⅰ)$|{log_2}0.6-0|=|{log_2}0.6|={log_2}\frac{5}{3},|{2^{0.6}}-0|=|{2^{0.6}}|={2^{0.6}}$.(1分)
∵$0<{log_2}\frac{5}{3}<1,1<{2^{0.6}}<2$,(2分)
∴${log_2}\frac{5}{3}<{2^{0.6}}$,
∴$|{log_2}0.6-0|<|{2^{0.6}}-0|$,
∴20.6比log20.6远离0.(3分)
(Ⅱ)$f(x)=\left\{\begin{array}{l}sinx,x∈(kπ+\frac{π}{4},kπ+\frac{3π}{4})(k∈Z)\\ cosx,x∈(kπ+\frac{3π}{4},kπ+\frac{5π}{4})(k∈Z).\end{array}\right.$(5分)f(x)的性质:
①f(x)既不是奇函数也不是偶函数;
②f(x)是周期函数,最小正周期T=2π;
③f(x)在区间$({2kπ+\frac{π}{4},2kπ+\frac{π}{2}}],[{2kπ+π,2kπ+\frac{5π}{4}}),[{2kπ+\frac{3π}{2},2kπ+\frac{7π}{4}})$,$({2kπ+\frac{7π}{4},2kπ+2π}](k∈Z)$单调递增,
f(x)在区间$[{2kπ,2kπ+\frac{π}{4}})$,$[{2kπ+\frac{π}{2},2kπ+\frac{3π}{4}}),({2kπ+\frac{3π}{4},2kπ+π}]$,$({2kπ+\frac{5π}{4},2kπ+\frac{3π}{2}}]$(k∈Z)单调递减;
④当x=2kπ或$x=2kπ+\frac{π}{2}(k∈Z)$时,f(x)有最大值1,
当x=2kπ+π或$x=2kπ+\frac{3π}{2}(k∈Z)$时,f(x)有最小值-1.(8分)
点评 本题考查了新定义“x比y远离m”、对数函数的单调性、三角函数的图象与性质,考查了推理能力与计算能力,属于中档题.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
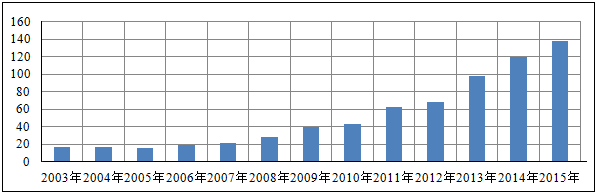
| A. | f(x)=ax2+bx+c | B. | f(x)=aex+b | C. | f(x)=eax+b | D. | f(x)=alnx+b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 5 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆的面积与半径具有相关性 | B. | 纯净度与净化次数不具有相关性 | ||
| C. | 作物的产量与人的耕耘是负相关 | D. | 学习成绩与学习效率是正相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 恰有1名男生与恰有2名女生 | B. | 至少有1名男生与全是男生 | ||
| C. | 至少有1名男生与至少有1名女生 | D. | 至少有1名男生与全是女生 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com