练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知向量，，若，的方向是沿方向绕着点按逆时针方向旋转角得到的，则称经过一次变换得到.已知向量经过一次变换后得到，经过一次变换后得到，…，如此下去，经过一次变换后得到，设，则__________.

    【答案】

    【解析】

    由题意可得经过一次变换得到，相当于一次旋转变换，利用矩阵变换得出，分别求得三次变换后得到的向量坐标，再由，可得向量经过2019次变换后得到，，即可得到所求值．

    解：由题意可得经过一次变换得到，相当于一次旋转变换

    得，

    而向量经过一次变换后得到，

    即为，可得向量，

    向量经过一次变换后得到，

    即有，可得向量，

    向量经过一次变换后得到，

    即为，可得向量，

    而，

    可得再经过三次变换后得到的向量坐标为，

    则向量经过2019次变换后得到，，，

    可得，

    故答案为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知为等差数列，各项为正的等比数列的前项和为，，，__________.在①；②；③这三个条件中任选其中一个，补充在横线上，并完成下面问题的解答（如果选择多个条件解答，则以选择第一个解答记分）.

    （1）求数列和的通项公式；

    （2）求数列的前项和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知的内角、、的对边分别为、、，且．

    （Ⅰ）求；

    （Ⅱ）若，，如图，为线段上一点，且，求的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】学校艺术节对四件参赛作品只评一件一等奖，在评奖揭晓前，甲，乙，丙，丁四位同学对这四件参赛作品预测如下：

    甲说：“是或作品获得一等奖”； 乙说：“ 作品获得一等奖”；

    丙说：“ 两件作品未获得一等奖”； 丁说：“是作品获得一等奖”．

    评奖揭晓后，发现这四位同学中只有两位说的话是对的，则获得一等奖的作品是_________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线，直线（）与交于两点，为的中点，为坐标原点．

    （1）求直线斜率的最大值；

    （2）若点在直线上，且为等边三角形，求点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以平面直角坐标系的原点为极点，轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程为，将曲线绕极点逆时针旋转后得到曲线.

    （Ⅰ）求曲线的极坐标方程；

    （Ⅱ）若直线：与，分别相交于异于极点的，两点，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝lg(x＋1)．

    (1)若0<f(1－2x)－f(x)<1，求实数x的取值范围；

    (2)若g(x)是以2为周期的偶函数，且当0≤x≤1时，有g(x)＝f(x)，当x∈[1,2]时，求函数y＝g(x)的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知椭圆上顶点为A，右焦点为F，直线与圆相切，其中.

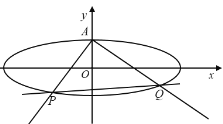
    （1）求椭圆的方程；

    （2）不过点A的动直线l与椭圆C相交于P，Q两点，且，证明：动直线l过定点，并且求出该定点坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正项数列满的前项和为，且满足.数列满足，.

    （1）求数列、的通项公式；

    （2）记数列满足设数列的前项和为，数列的前项和为，试比较与的大小

    查看答案和解析>>

    同步练习册答案