
【题目】已知正项数列![]() 满的前
满的前![]() 项和为
项和为![]() ,且满足
,且满足![]() .数列
.数列![]() 满足
满足![]() ,
,![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)记数列![]() 满足
满足![]() 设数列
设数列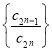 的前
的前![]() 项和为
项和为![]() ,数列
,数列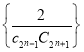 的前
的前![]() 项和为
项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小
的大小
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() ,若
,若![]() ,
,![]() 的方向是沿
的方向是沿![]() 方向绕着
方向绕着![]() 点按逆时针方向旋转
点按逆时针方向旋转![]() 角得到的,则称
角得到的,则称![]() 经过一次
经过一次![]() 变换得到
变换得到![]() .已知向量
.已知向量![]() 经过一次
经过一次![]() 变换后得到
变换后得到![]() ,
,![]() 经过一次
经过一次![]() 变换后得到
变换后得到![]() ,…,如此下去,
,…,如此下去,![]() 经过一次
经过一次![]() 变换后得到
变换后得到![]() ,设
,设![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解市民对电视剧市场的爱好,某上星电视台邀请了100位电视剧爱好者(男50人、女50人)对4月份观看其播出的电视剧集数进行调研,得到这100名电视剧爱好者观看集数的中位数为39集(假设这100名电视剧爱好者的观看集数均在![]() 集内),且观看集数在
集内),且观看集数在![]() 集内的人数为15,并根据调查结果画出如图所示的频率分布直方图.
集内的人数为15,并根据调查结果画出如图所示的频率分布直方图.

(1)求![]() ,
,![]() 的值;
的值;
(2)有些观众喜欢带有主角光环意识来观剧.但是最近几年的影视作品里出现了一个有趣的趋势——攻气十足的女性角色越来越讨人喜欢,傻白甜的女主们则破了主角光环,各种被嫌弃,更有些剧集中明明是女配的脚本,却因为更具有大女主气场,而获得了比主角更多的关注与声量,如《完美关系》里的斯黛拉,《精英律师》里的栗娜,《我的前半生》里的唐晶,……已知在这100名电视剧爱好者的女性中有31名认为自己有主角光环意识,男性中有19名认为自己有主角光环意识,根据以上数据请同学们制作出列联表,并且判断能否在犯错误的概率不超过0.001的前提下认为性别与是否观剧带有主角光环意识有关系?
参考公式及数据: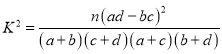 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年1月10日,中国工程院院士黄旭华和中国科学院院士曾庆存荣获2019年度国家最高科学技术奖.曾庆存院士是国际数值天气预报奠基人之一,他的算法是世界数值天气预报核心技术的基础,在气象预报中,过往的统计数据至关重要,如图是根据甲地过去50年的气象记录所绘制的每年高温天数(若某天气温达到35 ℃及以上,则称之为高温天)的频率分布直方图.若某年的高温天达到15天及以上,则称该年为高温年,假设每年是否为高温年相互独立,以这50年中每年高温天数的频率作为今后每年是否为高温年的概率.
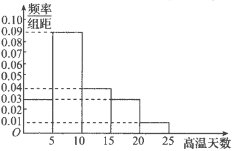
(1)求今后4年中,甲地至少有3年为高温年的概率.
(2)某同学在位于甲地的大学里勤工俭学,成为了校内奶茶店(消费区在户外)的店长,为了减少高温年带来的损失,该同学现在有两种方案选择:方案一:不购买遮阳伞,一旦某年为高温年,则预计当年的收入会减少6000元;方案二:购买一些遮阳伞,费用为5000元,可使用4年,一旦某年为高温年,则预计当年的收入会增加1000元.以4年为期,试分析该同学是否应该购买遮阳伞?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角系![]() 中,点A为曲线C:
中,点A为曲线C:![]() 在第一象限的图象上的动点,点E,G在曲线C的准线
在第一象限的图象上的动点,点E,G在曲线C的准线![]() 上,且点G在x轴的下方,圆O与准线相切,直线
上,且点G在x轴的下方,圆O与准线相切,直线![]() 交曲线C于点B,交圆O于点D,H.
交曲线C于点B,交圆O于点D,H.
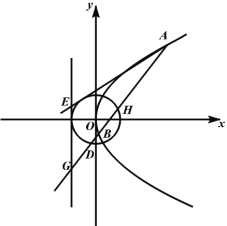
(1)当点H为曲线C的焦点,![]() 时,求
时,求![]() ;
;
(2)当点O为![]() 的内心时,若
的内心时,若![]() ,求点A的坐标.
,求点A的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记数列![]() 的前
的前![]() 项和为
项和为![]() ,若存在实数H,使得对任意的
,若存在实数H,使得对任意的![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为“和有界数列”.下列说法正确的是( )
为“和有界数列”.下列说法正确的是( )
A.若![]() 是等差数列,且公差
是等差数列,且公差![]() ,则
,则![]() 是“和有界数列”
是“和有界数列”
B.若![]() 是等差数列,且
是等差数列,且![]() 是“和有界数列”,则公差
是“和有界数列”,则公差![]()
C.若![]() 是等比数列,且公比
是等比数列,且公比![]() ,则
,则![]() 是“和有界数列”
是“和有界数列”
D.若![]() 是等比数列,且
是等比数列,且![]() 是“和有界数列”,则
是“和有界数列”,则![]() 的公比
的公比![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是空气质量的一个重要指标,我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35μg/m3以下空气质量为一级,在35μg/m3~75μg/m3之间空气质量为二级,在75μg/m3以上空气质量为超标.如图是某市2019年12月1日到10日PM2.5日均值(单位:μg/m3)的统计数据,则下列叙述不正确的是( )
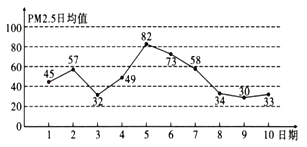
A.这10天中,12月5日的空气质量超标
B.这10天中有5天空气质量为二级
C.从5日到10日,PM2.5日均值逐渐降低
D.这10天的PM2.5日均值的中位数是47
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com