
【题目】甲、乙两人玩猜数字游戏,先由甲心中任想一个数字,记为![]() ,再由乙猜甲刚才想的数字把乙猜的数字记为
,再由乙猜甲刚才想的数字把乙猜的数字记为![]() ,且
,且![]() ,若
,若![]() ,则称甲乙“心有灵犀”,现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________
,则称甲乙“心有灵犀”,现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________
【答案】![]()
【解析】
试验发生的所有事件是从0,1,2,3,4,5,6,7,8,9十个数中任取两个数由分步计数原理知共有10×10种不同的结果,而满足条件的|a﹣b|≤2的情况通过列举得到共28种情况,代入公式得到结果.
试验发生的所有事件是从0,1,2,3,4,5,6,7,8,9十个数中任取两个共有10×10种不同的结果,
则|a﹣b|≤1的情况有0,0;1,1;2,2;3,3;4,4;5,5;6,6;7,7;8,8;9,9;
0,1;1,0;1,2;2,1;2,3;3,2;3,4;4,3;4,5;5,4;5,6;6,5;6,7;7,6;7,8;8,7;8,9;9,8共28种情况,
甲乙出现的结果共有10×10=100,
∴他们”心有灵犀”的概率为P![]() .
.
故答案为:![]()


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 上位于第一象限内的任意一点,
上位于第一象限内的任意一点,![]() 为坐标原点,
为坐标原点,![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,![]() ,圆
,圆![]() :
:![]() .
.
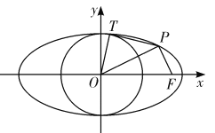
(1)求椭圆![]() 和圆
和圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作
作![]() 与圆
与圆![]() 相切于点
相切于点![]() ,使得点
,使得点![]() ,点
,点![]() 在
在![]() 的两侧.求四边形
的两侧.求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点作直线交抛物线于
的焦点作直线交抛物线于![]() ,
,![]() 两点,若
两点,若![]() ,则
,则![]() 的值为( )
的值为( )
A. 10 B. 8 C. 6 D. 4
【答案】B
【解析】
根据过抛物线焦点的弦长公式,利用题目所给已知条件,求得弦长![]() .
.
根据过抛物线焦点的弦长公式有![]() .故选B.
.故选B.
【点睛】
本小题主要考查过抛物线焦点的弦长公式,即![]() .要注意只有过抛物线焦点的弦长才可以使用.属于基础题.
.要注意只有过抛物线焦点的弦长才可以使用.属于基础题.
【题型】单选题
【结束】
10
【题目】已知椭圆![]() :
: ![]() 的右顶点、上顶点分别为
的右顶点、上顶点分别为![]() 、
、![]() ,坐标原点到直线
,坐标原点到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,则椭圆
,则椭圆![]() 的方程为( )
的方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图象关于直线
,其图象关于直线![]() 对称,为了得到函数
对称,为了得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象上的所有点( )
的图象上的所有点( )
A.先向左平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
B.先向右平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
C.先向右平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
D.先向左平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点的椭圆![]() 和抛物线
和抛物线![]() 有相同的焦点
有相同的焦点![]() ,椭圆
,椭圆![]() 过点
过点![]() ,抛物线
,抛物线![]() 的顶点为原点.
的顶点为原点.
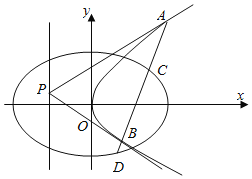
![]() 求椭圆
求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
![]() 设点P为抛物线
设点P为抛物线![]() 准线上的任意一点,过点P作抛物线
准线上的任意一点,过点P作抛物线![]() 的两条切线PA,PB,其中A,B为切点.
的两条切线PA,PB,其中A,B为切点.
![]() 设直线PA,PB的斜率分别为
设直线PA,PB的斜率分别为![]() ,
,![]() ,求证:
,求证:![]() 为定值;
为定值;
![]() 若直线AB交椭圆
若直线AB交椭圆![]() 于C,D两点,
于C,D两点,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的面积,试问:
的面积,试问:![]() 是否有最小值?若有,求出最小值;若没有,请说明理由.
是否有最小值?若有,求出最小值;若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年,教育部发文确定新高考改革正式启动,湖南、广东、湖北等8省市开始实行新高考制度,从2018年下学期的高一年级学生开始实行.为了适应新高考改革,某校组织了一次新高考质量测评,在成绩统计分析中,高二某班的数学成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题:
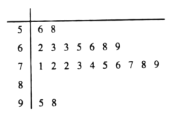
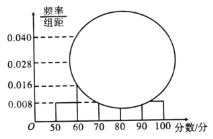
(1)求该班数学成绩在![]() 的频率及全班人数;
的频率及全班人数;
(2)根据频率分布直方图估计该班这次测评的数学平均分;
(3)若规定![]() 分及其以上为优秀,现从该班分数在
分及其以上为优秀,现从该班分数在![]() 分及其以上的试卷中任取
分及其以上的试卷中任取![]() 份分析学生得分情况,求在抽取的
份分析学生得分情况,求在抽取的![]() 份试卷中至少有
份试卷中至少有![]() 份优秀的概率.
份优秀的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com