
设F1、F2分别是椭圆 +y2=1的左、右焦点.
+y2=1的左、右焦点.
(1)若P是第一象限内该椭圆上的一点,且 =-
=- ,求点P的坐标;
,求点P的坐标;
(2)设过定点M(0,2)的直线l与椭圆交于不同的两点A、B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围.
解:(1)a=2,b=1,c= .∴F1(-
.∴F1(- ,0),F2(
,0),F2( ,0).
,0).
设P(x,y)(x>0,y>0).则 =(-
=(- -x,-y)(
-x,-y)( -x,-y)=x2+y2-3=-
-x,-y)=x2+y2-3=- ,又
,又 +y2=1,
+y2=1,
联立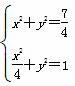 ,解得
,解得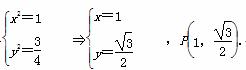
(2)显然x=0不满足题设条件.可设l的方程为y=kx+2,设A(x1,y1),B(x2,y2).
联立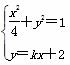 ⇒x2+4(kx+2)2=4
⇒x2+4(kx+2)2=4
⇒(1+4k2)x2+16kx+12=0
∴x1x2=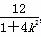 ,x1+x2=-
,x1+x2=-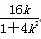
由Δ=(16k)2-4·(1+4k2)·12>0
16k2-3(1+4k2)>0,4k2-3>0,得k2> .①
.①
又∠AOB为锐角⇔cos∠AOB>0⇔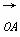 ·
·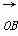 >0,
>0,
∴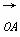 ·
·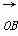 =x1x2+y1y2>0
=x1x2+y1y2>0
又y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4
∴x1x2+y1y2=(1+k2)x1x2+2k(x1+x2)+4
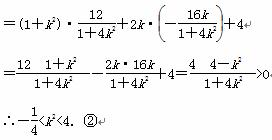 综合①②可知
综合①②可知 <k2<4,∴k的取值范围是
<k2<4,∴k的取值范围是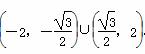 .
.


科目:高中数学 来源: 题型:
已知{an}是公差为d的等差数列,它的前n项和为Sn,S4=2S2+8.
(1)求公差d的值;
(2)若a1=1,设Tn是数列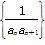 的前n项和,求使不等式Tn≥
的前n项和,求使不等式Tn≥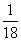 (m2-5m)对所有的n∈N*恒成立的最大正整数m的值;
(m2-5m)对所有的n∈N*恒成立的最大正整数m的值;
(3)设bn=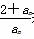 若对任意的n∈N*,都有bn≤b4成立,求a1的取值范围.
若对任意的n∈N*,都有bn≤b4成立,求a1的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
斜率为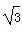 的直线与双曲线
的直线与双曲线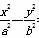 =1(a>0,b>0)恒有两个公共点,则双曲线离心率的取值范围是( )
=1(a>0,b>0)恒有两个公共点,则双曲线离心率的取值范围是( )
A.[2,+∞) B.(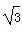 ,+∞)
,+∞)
C.(1,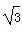 ) D.(2,+∞)
) D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为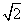 ,且过点(4,-
,且过点(4,-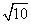 ).点M(3,m)在双曲线上.
).点M(3,m)在双曲线上.
(1)求双曲线方程;
(2)求证: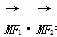 =0;
=0;
(3)求△F1MF2面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
设动点P在直线x-1=0上,O为坐标原点,以OP为直角边,点O为直角顶点作等腰直角三角形OPQ,则动点Q的轨迹是( )
A.椭圆 B.两条平行直线
C.抛物线 D.双曲线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com