
分析 分x=0,0<x≤1,两种情况进行讨论,分离出参数a后转化为函数求最值即可,利用导数即可求得函数最值,注意最后要对a取交集.
解答 解:当x=0时,不等式ax3-x2+4x+3≥0对任意a∈R恒成立;
当0<x≤1时,ax3-x2+4x+3≥0可化为a≥$\frac{1}{x}$-$\frac{4}{{x}^{2}}$-$\frac{3}{{x}^{3}}$,
令f(x)=$\frac{1}{x}$-$\frac{4}{{x}^{2}}$-$\frac{3}{{x}^{3}}$,则f′(x)=-$\frac{1}{{x}^{2}}$+$\frac{8}{{x}^{3}}$+$\frac{9}{{x}^{4}}$=-$\frac{(x-9)(x+1)}{{x}^{4}}$(*),
当0<x≤1时,f′(x)>0,f(x)在(0,1]上单调递增,
f(x)max=f(1)=-6,
∴a≥-6;
综上所述,实数a的取值范围是a≥-6.
点评 本题考查利用导数研究函数的最值,考查转化思想、分类与整合思想,按照自变量讨论,最后要对参数范围取交集.若按照参数讨论则取并集,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
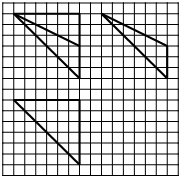 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,则该零件的表面积为(单位:cm2)( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,则该零件的表面积为(单位:cm2)( )| A. | $27\sqrt{2}+9\sqrt{5}+9$ | B. | $27\sqrt{2}+18\sqrt{5}$ | C. | $9\sqrt{2}+9\sqrt{5}+27$ | D. | $36+9\sqrt{5}+18\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
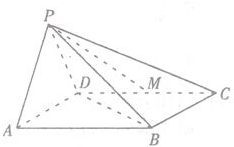 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 第4天 | 第8天 | 第16天 | 第22天 |
| 价格(元) | 23 | 24 | 22 | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2-i | B. | 2+i | C. | 1-2i | D. | 1+2i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com