
【题目】设公差不为0的等差数列{an}的前n项和为Sn , 若a2 , a5 , a11成等比数列,且a11=2(Sm﹣Sn)(m>n>0,m,n∈N*),则m+n的值是 .
【答案】9
【解析】解:设公差d不为0的等差数列{an}, a2 , a5 , a11成等比数列,
可得a52=a2a11 ,
即为(a1+4d)2=(a1+d)(a1+10d),
化简可得a1=2d,
a11=2(Sm﹣Sn),
即有12d=2[ma1+ ![]() d﹣na1﹣
d﹣na1﹣ ![]() d],
d],
12d=4md﹣4nd+d(m2﹣m﹣n2+n),
即有(m﹣n)(m+n+3)=12,
由于m>n>0,m,n∈N*,
可得m+n+3≥6,m﹣n≤2,
若m=2,3,n=1则方程不成立;
若m=3,4,n=2,则方程不成立;
若m=4,5,n=3,则方程不成立;
若m=5,n=4,则方程成立;
m=6,n=4则方程不成立.
故m+n=5+4=9.
故答案为:9.
设公差d不为0的等差数列{an},运用等比数列中项的性质,化简可得a1=2d,再由等差数列的求和公式,化简可得(m﹣n)(m+n+3)=12,通过m>n,且m,n为自然数,列举判断即可得到所求和.


科目:高中数学 来源: 题型:
【题目】我国古代有着辉煌的数学研究成果.《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、…、《辑古算经》等算经十书,有着十分丰富多彩的内容,是了解我国古代数学的重要文献.这10部专著中有7部产生于魏晋南北朝时期.某中学拟从这10部名著中选择2部作为“数学文化”校本课程学习内容,则所选2部名著中至少有一部是魏晋南北朝时期的名著的概率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4sinxcos2( ![]() +
+ ![]() )﹣cos2x.
)﹣cos2x.
(1)将函数y=f(2x)的图象向右平移 ![]() 个单位长度得到函数y=g(x)的图象,求函数g(x)在x∈[
个单位长度得到函数y=g(x)的图象,求函数g(x)在x∈[ ![]() ,
, ![]() ]上的值域;
]上的值域;
(2)已知a,b,c分别为△ABC中角A,B,C的对边,且满足b=2,f(A)= ![]() a=2bsinA,B∈(0,
a=2bsinA,B∈(0, ![]() ),求△ABC的面积.
),求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m、n是两条不同的直线,α、β是两个不同的平面,给出下列命题: ①若α⊥β,m∥α,则m⊥β;
②若m⊥α,n⊥β,且m⊥n,则α⊥β;
③若m⊥β,m∥α,则α⊥β;
④若m∥α,n∥β,且m∥n,则α∥β.
其中正确命题的序号是( )
A.①④
B.②③
C.②④
D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() ,曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直.
,曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直.
(1)求a的值;
(2)若对于任意的x∈[1,+∞),f(x)≤m(x﹣1)恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD. 
(Ⅰ)求证:CD⊥AM;
(Ⅱ)若AM=BC=2,求直线AM与平面BDM所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函f(x)=lnx﹣ax2+(2﹣a)x. ①讨论f(x)的单调性;
②设a>0,证明:当0<x< ![]() 时,
时, ![]() ;
;
③函数y=f(x)的图象与x轴相交于A、B两点,线段AB中点的横坐标为x0 , 证明f′(x0)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地要建造一个边长为2(单位:km)的正方形市民休闲公园OABC,将其中的区域ODC开挖成一个池塘,如图建立平面直角坐标系后,点D的坐标为(1,2),曲线OD是函数y=ax2图象的一部分,对边OA上一点M在区域OABD内作一次函数y=kx+b(k>0)的图象,与线段DB交于点N(点N不与点D重合),且线段MN与曲线OD有且只有一个公共点P,四边形MABN为绿化风景区: 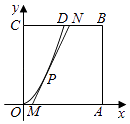
(1)求证:b=﹣ ![]() ;
;
(2)设点P的横坐标为t,①用t表示M、N两点坐标;②将四边形MABN的面积S表示成关于t的函数S=S(t),并求S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com