Question

14．设函数f（x）对任意实数x满足f（x）=-f（x+1），且当0≤x≤1时，f（x）=x（1-x），若关于x的方程f（x）=kx有3个不同的实数根，则k的取值范围是（5-2$\sqrt{6}$，1）∪{2$\sqrt{2}-3$}．

Answer 1

分析 先确定函数f（x）为周期函数，再将问题等价方程f（x）仅有唯一实数根，并结合函数的图象与判别式得出k的取值范围．

解答 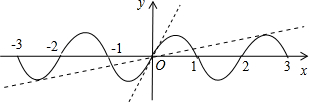解：∵f（x）=-f（x+1），∴f（x+2）=f（x），
即f（x）是以2为周期的函数，
因为，当x∈[0，1]时，f（x）=x（1-x），
所以，x∈[-1，0]时，x+1∈[0，1]，
所以，f（x）=-f（x+1）=x（x+2），
∴f（x）在一个周期内的解析式为f（x）=$\left\{\begin{array}{l}{x（1-x），x∈[0，1]}\\{x（1+x），x∈[-1，0]}\end{array}\right.$，如右图，
依题意，方程f（x）=kx有三个不等的实根，
则该方程一根为负，一根为正，一根为0，即f（x）=kx只有唯一一个正实数根，
当x∈[2，3]时，x-2∈[0，1]，
所以，f（x）=f（x-2）=（x-2）（3-x），
令（x-2）（3-x）=kx，整理得，x²+（k-5）x+6=0，
由△=0，解得k=5-4$\sqrt{6}$（舍k=5+4$\sqrt{6}$），
此时，直线y=（5-4$\sqrt{6}$）x与f（x）的图象相切，共有5个交点，如图长虚线直线，
所以，k＞5-4$\sqrt{6}$，------------------①
另一方面，函数f（x）=x（1-x）在x=0处的导数为f'（0）=1，
即直线y=x与f（x）的图象只有一个交点，如图短虚直线，
所以，k＜1，------------------------②
当1＜x＜2时，-1＜x-2＜0，f（x-2）=（x-2）（x-1），可得f（x）=f（x-2）=x²-3x+2，
由x²-3x+2=kx，可得判别式为（3+k）²-8=0，
解得k=2$\sqrt{2}$-3（-2$\sqrt{2}$-3舍去），
当直线y=kx（k＜0）与y=f（x）相切可得2$\sqrt{2}$-3．
综合以上讨论得，k∈（5-2$\sqrt{6}$，1）．
故答案为：（5-2$\sqrt{6}$，1）∪{2$\sqrt{2}-3$}．

点评 本题主要考查了抽象函数及其应用，涉及函数周期性的判断与应用，函数的图象与性质，以及函数零点个数的判断，属于中档题．